《2020年新教材高中物理 必備考點(diǎn) 素養(yǎng)評(píng)價(jià)6(含解析)新人教版必修2》由會(huì)員分享�����,可在線閱讀���,更多相關(guān)《2020年新教材高中物理 必備考點(diǎn) 素養(yǎng)評(píng)價(jià)6(含解析)新人教版必修2(8頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1��、必備考點(diǎn)·素養(yǎng)評(píng)價(jià)6
素養(yǎng)一 物理觀念
考點(diǎn)圓周運(yùn)動(dòng)各物理量間的關(guān)系
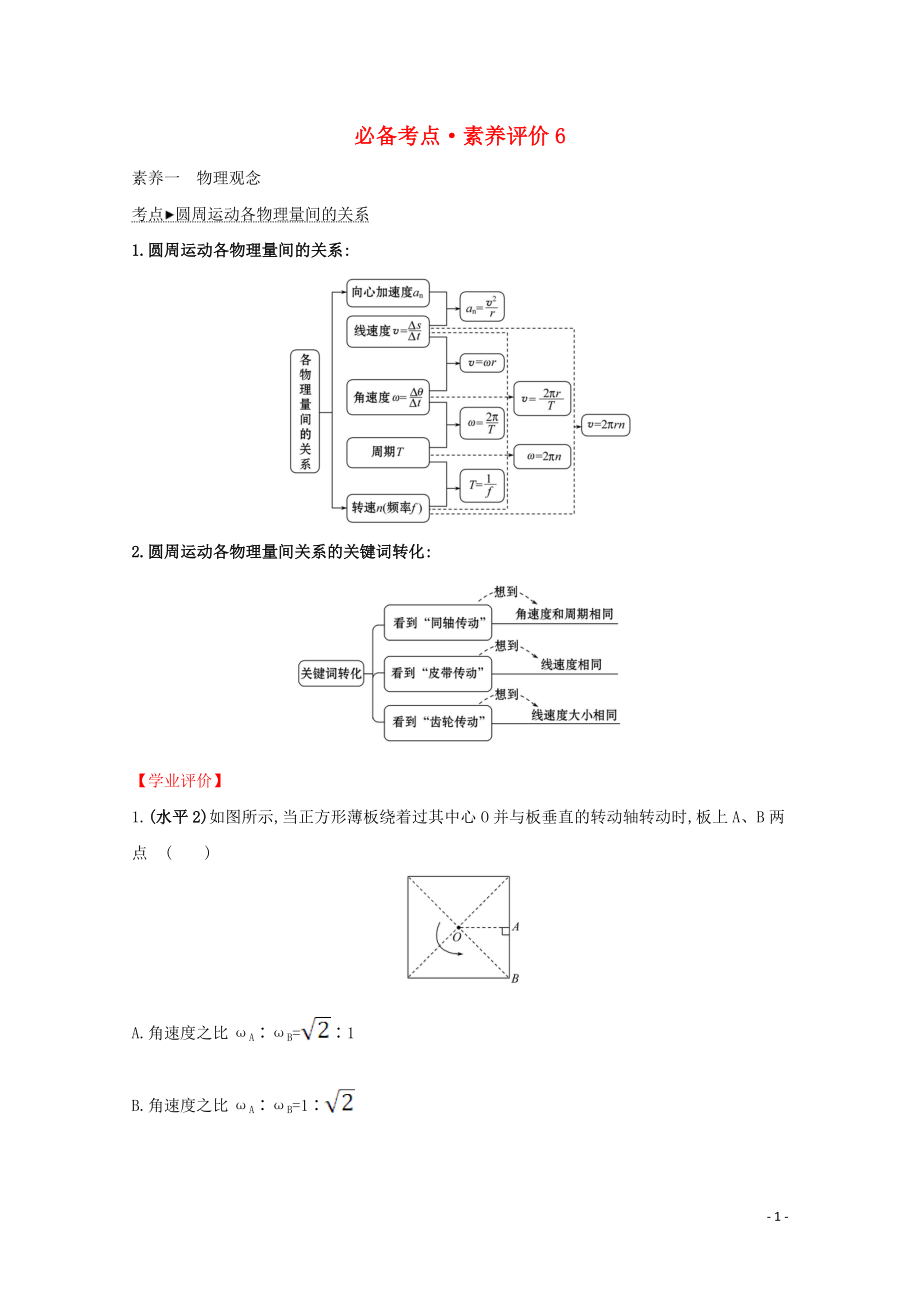
1.圓周運(yùn)動(dòng)各物理量間的關(guān)系:
2.圓周運(yùn)動(dòng)各物理量間關(guān)系的關(guān)鍵詞轉(zhuǎn)化:
【學(xué)業(yè)評(píng)價(jià)】
1.(水平2)如圖所示,當(dāng)正方形薄板繞著過其中心O并與板垂直的轉(zhuǎn)動(dòng)軸轉(zhuǎn)動(dòng)時(shí),板上A�、B兩點(diǎn) ( )
A.角速度之比ωA∶ωB=∶1
B.角速度之比ωA∶ωB=1∶
C.線速度之比vA∶vB=∶1
D.線速度之比vA∶vB=1∶
【解析】選D。板上A��、B兩點(diǎn)的角速度相等,角速度之比ωA∶ωB=1∶1,選項(xiàng)A���、B錯(cuò)誤;線速度v=ωr,線速度之比vA∶vB=1∶,選項(xiàng)C錯(cuò)誤,D正確����。
2.(水平4)如圖所示
2、,一位同學(xué)玩飛鏢游戲����。圓盤最上端有一點(diǎn)P,飛鏢拋出時(shí)與P等高,且距離P點(diǎn)為L(zhǎng)。當(dāng)飛鏢以初速度v0垂直盤面瞄準(zhǔn)P點(diǎn)拋出的同時(shí),圓盤以經(jīng)過盤心O點(diǎn)的水平線為軸在豎直平面內(nèi)勻速轉(zhuǎn)動(dòng)�。忽略空氣阻力,重力加速度為g,若飛鏢恰好擊中P點(diǎn),則 ( )
A.飛鏢擊中P點(diǎn)所需的時(shí)間大于
B.圓盤的半徑可能為
C.P點(diǎn)隨圓盤轉(zhuǎn)動(dòng)的線速度可能為
D.圓盤轉(zhuǎn)動(dòng)角速度的最小值為
【解析】選C。飛鏢水平位移為L(zhǎng),且水平方向?yàn)閯蛩龠\(yùn)動(dòng),所以飛行時(shí)間一定是,A錯(cuò)誤;豎直方向飛鏢做自由落體運(yùn)動(dòng),所以下落的高度為h=gt2=,要擊中P點(diǎn),P點(diǎn)一定是位于最下方,所以2R=h,R=,B錯(cuò)誤;P點(diǎn)轉(zhuǎn)到最下方可能經(jīng)過的圈
3����、數(shù)為,其中n=0,1,2…,所以線速度的可能值為v==,當(dāng)n=2時(shí),v=,C正確;而ω==,當(dāng)n=0時(shí),得最小角速度ω=,D錯(cuò)誤。
素養(yǎng)二 科學(xué)思維
考點(diǎn)1圓周運(yùn)動(dòng)的動(dòng)力學(xué)分析
1.圓周運(yùn)動(dòng)動(dòng)力學(xué)分析思路:
向心力公式是牛頓第二定律對(duì)圓周運(yùn)動(dòng)的應(yīng)用,求解圓周運(yùn)動(dòng)的動(dòng)力學(xué)問題與應(yīng)用牛頓第二定律的解題思路相同,但要注意幾個(gè)特點(diǎn):
(1)向心力是沿半徑方向的合力,是效果力,不是實(shí)際受力�����。
(2)向心力公式有多種形式:F=m=mω2r=mr,要根據(jù)已知條件選用����。
(3)正交分解時(shí),要注意圓心的位置,沿半徑方向和切線方向分解�。
2.圓周運(yùn)動(dòng)動(dòng)力學(xué)分析的關(guān)鍵詞轉(zhuǎn)化:
【學(xué)業(yè)評(píng)價(jià)】
4、1.(水平2)(多選)如圖所示,一根細(xì)線下端拴一個(gè)金屬小球P,細(xì)線的上端固定在金屬塊Q上,Q放在帶小孔的水平桌面上,小球在某一水平面內(nèi)做勻速圓周運(yùn)動(dòng)(圓錐擺)?,F(xiàn)使小球改到一個(gè)更高一些的水平面上做勻速圓周運(yùn)動(dòng)(圖上未畫出),兩次金屬塊Q都保持在桌面上靜止,則后一種情況與原來相比較,下列說法中正確的是 ( )
A.Q受到桌面的支持力變大
B.Q受到桌面的靜摩擦力變大
C.小球P運(yùn)動(dòng)的線速度變小
D.小球P運(yùn)動(dòng)的角速度變大
【解析】選B、D。金屬塊Q保持在桌面上靜止,對(duì)于金屬塊Q和小球P整體豎直方向上沒有加速度,根據(jù)平衡條件知,Q受到桌面的支持力等于兩物體的重力保持不變,故A錯(cuò)誤;
5�����、設(shè)細(xì)線與豎直方向的夾角為θ,細(xì)線的拉力大小為FT,細(xì)線的長(zhǎng)度為L(zhǎng),小球P做勻速圓周運(yùn)動(dòng)時(shí),由重力和細(xì)線的拉力的合力提供向心力,如圖所示,則有FT=,Fn=mgtanθ=mω2Lsinθ=m,解得ω=,
v=,使小球改到一個(gè)更高一些的水平面上做勻速圓周運(yùn)動(dòng)時(shí),θ增大,cosθ減小,sinθ��、tanθ增大,則細(xì)線拉力FT增大,角速度增大,線速度增大,故選項(xiàng)D正確,C錯(cuò)誤;對(duì)Q由平衡條件得Ff=FTsinθ,Q受到桌面的靜摩擦力變大,故B正確���。
2.(水平4)如圖所示,長(zhǎng)度均為l=1 m的兩根輕繩,一端共同系住質(zhì)量為m=0.5 kg的小球,另一端分別固定在等高的A�����、B兩點(diǎn),A����、B兩點(diǎn)間的距離
6�、也為l,重力加速度g取10 m/s2。現(xiàn)使小球在豎直平面內(nèi)以AB為軸做圓周運(yùn)動(dòng),若小球在最高點(diǎn)速率為v時(shí),每根繩的拉力恰好為零,則小球在最高點(diǎn)速率為2v時(shí),每根繩的拉力大小為 ( )
A.5 N B. N C.15 N D.10 N
【解析】選A���。小球在最高點(diǎn)速率為v時(shí),兩根繩的拉力恰好均為零,由牛頓第二定律得mg=m,當(dāng)小球在最高點(diǎn)的速率為2v時(shí),由牛頓第二定律得mg+2FTcos30°=m,解得FT=mg=5 N,故選項(xiàng)A正確��。
考點(diǎn)2臨界和極值問題
1.臨界極值問題的分類:
情境
小球在豎直面內(nèi)做圓周運(yùn)動(dòng)恰好通過最高點(diǎn)
物體隨圓盤一起做勻速圓周運(yùn)動(dòng),
7�����、剛好無相對(duì)滑動(dòng)
繩子能夠承受的最大拉力
模型建構(gòu)
分析
方法
假設(shè)法
圖解法
2.圓周運(yùn)動(dòng)的關(guān)鍵詞轉(zhuǎn)化:
【學(xué)業(yè)評(píng)價(jià)】
1.(水平2)如圖所示,長(zhǎng)為L(zhǎng)的細(xì)繩,一端系一質(zhì)量為m的小球,另一端固定在O點(diǎn),當(dāng)小球靜止時(shí)繩沿著豎直方向?����,F(xiàn)給小球一水平初速度v0,使小球在豎直平面內(nèi)做圓周運(yùn)動(dòng),并且剛好能夠通過最高點(diǎn),下列說法正確的是 ( )
A.小球通過最高點(diǎn)時(shí)速度為0
B.小球通過最高點(diǎn)時(shí)速度大小為
C.小球通過最低點(diǎn)時(shí)繩對(duì)小球的拉力為mg
D.小球通過最低點(diǎn)時(shí)繩對(duì)小球的拉力為
【解析】選B���。小球恰好經(jīng)過最高點(diǎn),速度取最小值,故只受重力,重力提供向心力
8��、:mg=m,解得:v=,故A錯(cuò)誤,B正確;小球在最低點(diǎn)時(shí),T-mg=m,解得:
T=mg+m,故C�、D錯(cuò)誤�。
2.(水平4)如圖,豎直環(huán)A半徑為r,固定在木板B上,木板B放在水平地面上,B的左右兩側(cè)各有一擋板固定在地上,B不能左右運(yùn)動(dòng),在環(huán)的最低點(diǎn)靜放有一小球C,A、B���、C的質(zhì)量均為m,現(xiàn)給小球一水平向右的瞬時(shí)速度v,小球會(huì)在環(huán)內(nèi)側(cè)做圓周運(yùn)動(dòng),為保證小球能通過環(huán)的最高點(diǎn),且不會(huì)使環(huán)在豎直方向上跳起(不計(jì)小球與環(huán)的摩擦阻力),小球在最高點(diǎn)的瞬時(shí)速度必須滿足
( )
A.最大值 B.最大值
C.最大值 D.最大值2
【解析】選C�����。考慮恰好不跳起的臨界情況,對(duì)球分
9����、析,根據(jù)牛頓第二定律,有:N+mg=m,其中:N=2mg,聯(lián)立解得:v1=,故A、B��、D項(xiàng)錯(cuò)誤,C項(xiàng)正確。
【補(bǔ)償訓(xùn)練】
如圖所示,底角為θ=的圓錐體靜止不動(dòng),頂端通過一根長(zhǎng)為l=1.25 m的細(xì)線懸掛一個(gè)質(zhì)量為m=1 kg的小球,細(xì)線處于張緊狀態(tài),若小球在水平面內(nèi)做勻速圓周運(yùn)動(dòng)的角速度為ω=4 rad/s,不計(jì)一切阻力,g=10 m/s2,則小球的向心加速度為
( )
A.10 m/s2 B.10 m/s2
C.15 m/s2 D.20 m/s2
【解析】選B�。
當(dāng)小球?qū)A錐體剛好無壓力時(shí),
向心力F=mgcotθ=mω2lcosθ,
解得:<ω=4 rad/s
所以當(dāng)ω=4 rad/s時(shí),小球離開斜面,設(shè)繩子與豎直方向的夾角為α,則
mgtanα=mω2lsinα,代入數(shù)據(jù)得cosα=0.5
小球的向心加速度:a=ω2lsinα=10 m/s2,故B正確。
- 8 -
 2020年新教材高中物理 必備考點(diǎn) 素養(yǎng)評(píng)價(jià)6(含解析)新人教版必修2
2020年新教材高中物理 必備考點(diǎn) 素養(yǎng)評(píng)價(jià)6(含解析)新人教版必修2