《2022年中考數(shù)學(xué)總復(fù)習(xí) 提分專練03 一次函數(shù)與反比例函數(shù)的綜合練習(xí) 湘教版》由會員分享����,可在線閱讀,更多相關(guān)《2022年中考數(shù)學(xué)總復(fù)習(xí) 提分專練03 一次函數(shù)與反比例函數(shù)的綜合練習(xí) 湘教版(7頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�����。
1、2022年中考數(shù)學(xué)總復(fù)習(xí) 提分專練03 一次函數(shù)與反比例函數(shù)的綜合練習(xí) 湘教版
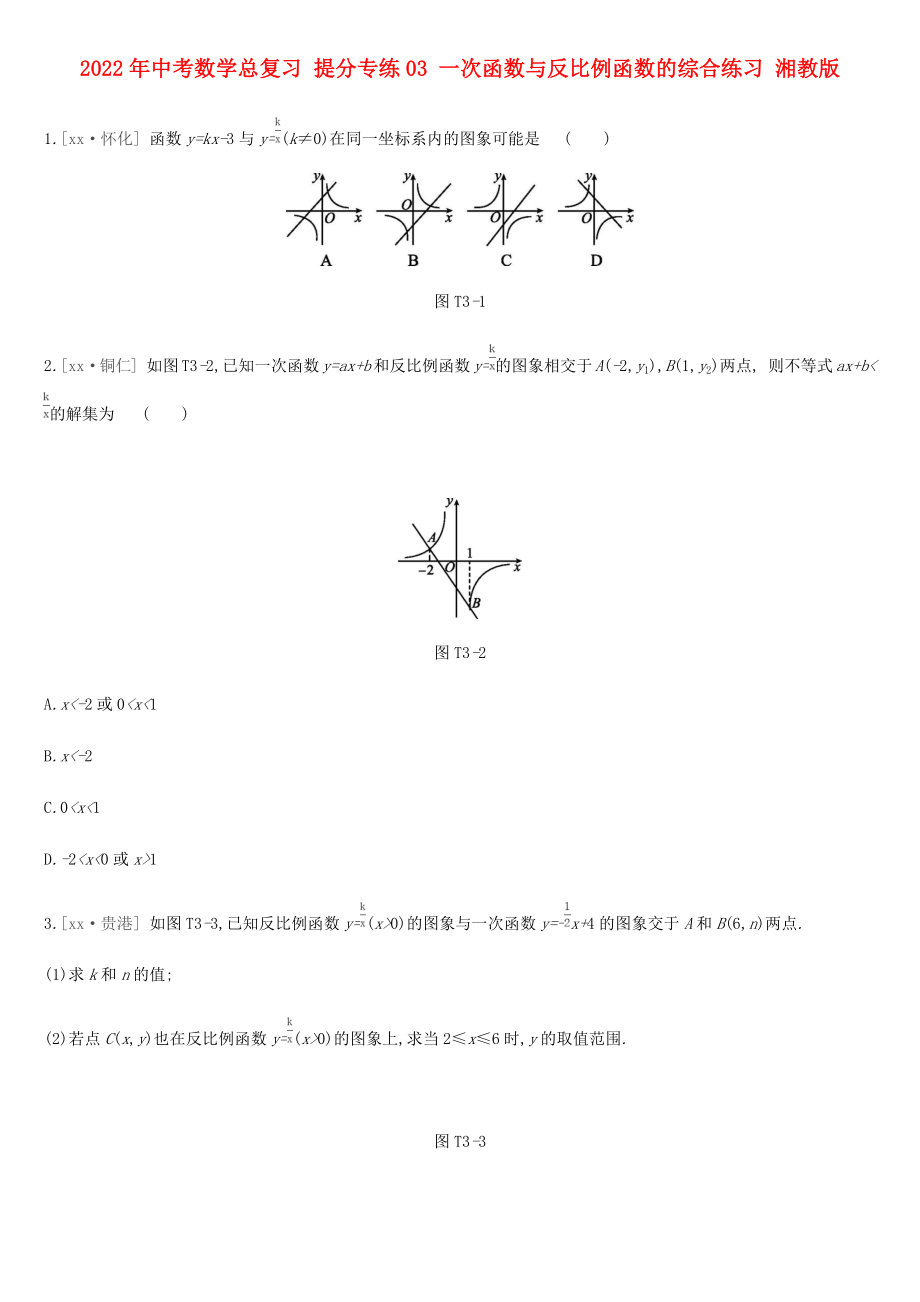
1.[xx·懷化] 函數(shù)y=kx-3與y=(k≠0)在同一坐標(biāo)系內(nèi)的圖象可能是 ( )
圖T3-1
2.[xx·銅仁] 如圖T3-2,已知一次函數(shù)y=ax+b和反比例函數(shù)y=的圖象相交于A(-2,y1),B(1,y2)兩點(diǎn), 則不等式ax+b<的解集為 ( )
圖T3-2
A.x<-2或01
3.[xx·貴港] 如圖T3-3,已知反比例函數(shù)y=(x>0)的圖象與一次函數(shù)y=-x+4的圖象交于A和B(6,n)兩點(diǎn).
2�����、(1)求k和n的值;
(2)若點(diǎn)C(x,y)也在反比例函數(shù)y=(x>0)的圖象上,求當(dāng)2≤x≤6時,y的取值范圍.
圖T3-3
4.[xx·咸寧] 如圖T3-4,在平面直角坐標(biāo)系中,矩形OABC的頂點(diǎn)B的坐標(biāo)為(4,2),直線y=-x+與邊AB,BC分別相交于點(diǎn)M,N,函數(shù)y=(x>0)的圖象過點(diǎn)M.
(1)試說明點(diǎn)N也在函數(shù)y=(x>0)的圖象上;
(2)將直線MN沿y軸的負(fù)方向平移得到直線M'N',當(dāng)直線M'N'與函數(shù)y=(x>0)的圖象僅有一個交點(diǎn)時,求直線M'N'的表達(dá)式.
圖T3-4
5.[xx·葫蘆島] 如圖T3-5,一次函
3����、數(shù)y=kx+b(k≠0)的圖象與反比例函數(shù)y=(a≠0)的圖象在第二象限交于點(diǎn)A(m,2),與x軸交于點(diǎn)C(-1,0),過點(diǎn)A作AB⊥x軸于點(diǎn)B,△ABC的面積是3.
(1)求一次函數(shù)和反比例函數(shù)的表達(dá)式;
(2)若直線AC與y軸交于點(diǎn)D,求△ABD的面積.
圖T3-5
6.[xx·株洲] 如圖T3-6,Rt△PAB的直角頂點(diǎn)P(3,4)在函數(shù)y=(x>0)的圖象上,頂點(diǎn)A,B在函數(shù)y=(x>0,0
4、t的表達(dá)式;
(2)若用Wmax和Wmin分別表示函數(shù)W的最大值和最小值,令T=Wmax+a2-a,其中a為實(shí)數(shù),求Tmin.
圖T3-6
7.[xx·株洲] 如圖T3-7,已知函數(shù)y=(k>0,x>0)的圖象與一次函數(shù)y=mx+5(m<0)的圖象相交于不同的兩點(diǎn)A,B,過點(diǎn)A作AD⊥x軸于點(diǎn)D,連接AO,其中點(diǎn)A的橫坐標(biāo)為x0,△AOD的面積為2.
(1)求k的值及x0=4時m的值;
(2)記[x]表示不超過x的最大整數(shù),例如:[1.4]=1,[2]=2,設(shè)t=OD·DC,若-
5�����、.B
2.D [解析] 觀察函數(shù)圖象可知,當(dāng)-21時,直線y=ax+b在雙曲線y=下方,即不等式ax+b<中x的取值范圍是-21.
3.解:(1)把B(6,n)代入一次函數(shù)y=-x+4中,可得n=-×6+4=1,所以n的值為1,B點(diǎn)的坐標(biāo)為(6,1),又B在反比例函數(shù)y=(x>0)的圖象上,所以k=xy=1×6=6,所以k的值為6.
(2)由(1)知反比例函數(shù)的表達(dá)式為y=,當(dāng)x=2時,y==3;當(dāng)x=6時,y==1,由函數(shù)圖象可知,當(dāng)2≤x≤6時,1≤y≤3.
4.解:(1)∵矩形OABC的頂點(diǎn)B的坐標(biāo)為(4,2),
∴點(diǎn)M的橫坐標(biāo)為4,點(diǎn)N的縱坐標(biāo)為2
6�����、,
把x=4代入y=-x+,得y=,
∴點(diǎn)M的坐標(biāo)為4,.
把y=2代入y=-x+,得x=1,
∴點(diǎn)N的坐標(biāo)為(1,2).
∵函數(shù)y=(x>0)的圖象過點(diǎn)M,
∴k=4×=2,∴y=(x>0).
把N(1,2)代入y=,得2=2,
∴點(diǎn)N也在函數(shù)y=(x>0)的圖象上.
(2)設(shè)直線M'N'的表達(dá)式為y=-x+b,
由得x2-2bx+4=0,
∵直線y=-x+b與函數(shù)y=(x>0)的圖象僅有一個交點(diǎn),
∴(-2b)2-4×4=0,
解得b1=2,b2=-2(舍去),
∴直線M'N'的表達(dá)式為y=-x+2.
5.解:(1)∵一次函數(shù)y=kx+b(k≠0)的圖象與反比
7�����、例函數(shù)y=(a≠0)的圖象在第二象限交于點(diǎn)A(m,2),與x軸交于點(diǎn)C(-1,0),∴點(diǎn)A,2.∵△ABC的面積是3,∴3=·AB·BC,即3=×2×-1-,解得a=-8,∴反比例函數(shù)的表達(dá)式為y=,∴A(-4,2).把A(-4,2),C(-1,0)的坐標(biāo)代入y=kx+b,得解得∴一次函數(shù)的表達(dá)式為y=-x-.
(2)∵直線AC與y軸交于點(diǎn)D,∴D0,-,∴OD=,∴S△ABD=×BC×(AB+OD)=×3×2+=4.
6.解:(1)∵y=的圖象經(jīng)過點(diǎn)P(3,4),∴k=12.
∵點(diǎn)P(3,4),PB∥x軸,∠BPA=90°,
∴A3,,B,4,
∴PA=4-,PB=3-,
∴S△
8��、PAB=PA·PB=4-3-=-t+6.
∵S△OPA=×3×4-=6-t,
∴W=S△OPA-S△PAB=6-t--t+6=-+t.
(2)∵W=-+t,
∴當(dāng)t=×12=6時,W取最大值,Wmax=.
∴T=+a2-a=a2-a+,
∴當(dāng)a=時,T取最小值,Tmin=.
7.解:(1)∵S△AOD=2,∴k=4,
∴y=.
∵x0=4,
∴y==1,
∴A(4,1).
將點(diǎn)A的坐標(biāo)代入y=mx+5(m<0),
得m=-1.
(2)由一次函數(shù)y=mx+5(m<0)可得點(diǎn)C的坐標(biāo)為-,0,
∴OC=-.
將Ax0,代入y=mx+5(m<0),
得mx0+5=,∴m+5x0=4.
∵OD=x0,OC=-,
∴CD=OC-OD=--x0.
∵t=OD·CD,
∴t=x0--x0=-x0+=-,
∴[m2t]==[-4m].
∵-
 2022年中考數(shù)學(xué)總復(fù)習(xí) 提分專練03 一次函數(shù)與反比例函數(shù)的綜合練習(xí) 湘教版
2022年中考數(shù)學(xué)總復(fù)習(xí) 提分專練03 一次函數(shù)與反比例函數(shù)的綜合練習(xí) 湘教版