2019-2020學年高中數(shù)學 第四章 指數(shù)函數(shù)與對數(shù)函數(shù) 4.4.1 對數(shù)函數(shù)的概念 4.4.2 對數(shù)函數(shù)的圖象和性質課后篇鞏固提升（含解析）新人教A版必修1

《2019-2020學年高中數(shù)學 第四章 指數(shù)函數(shù)與對數(shù)函數(shù) 4.4.1 對數(shù)函數(shù)的概念 4.4.2 對數(shù)函數(shù)的圖象和性質課后篇鞏固提升（含解析）新人教A版必修1》由會員分享，可在線閱讀，更多相關《2019-2020學年高中數(shù)學 第四章 指數(shù)函數(shù)與對數(shù)函數(shù) 4.4.1 對數(shù)函數(shù)的概念 4.4.2 對數(shù)函數(shù)的圖象和性質課后篇鞏固提升（含解析）新人教A版必修1（6頁珍藏版）》請在裝配圖網上搜索。

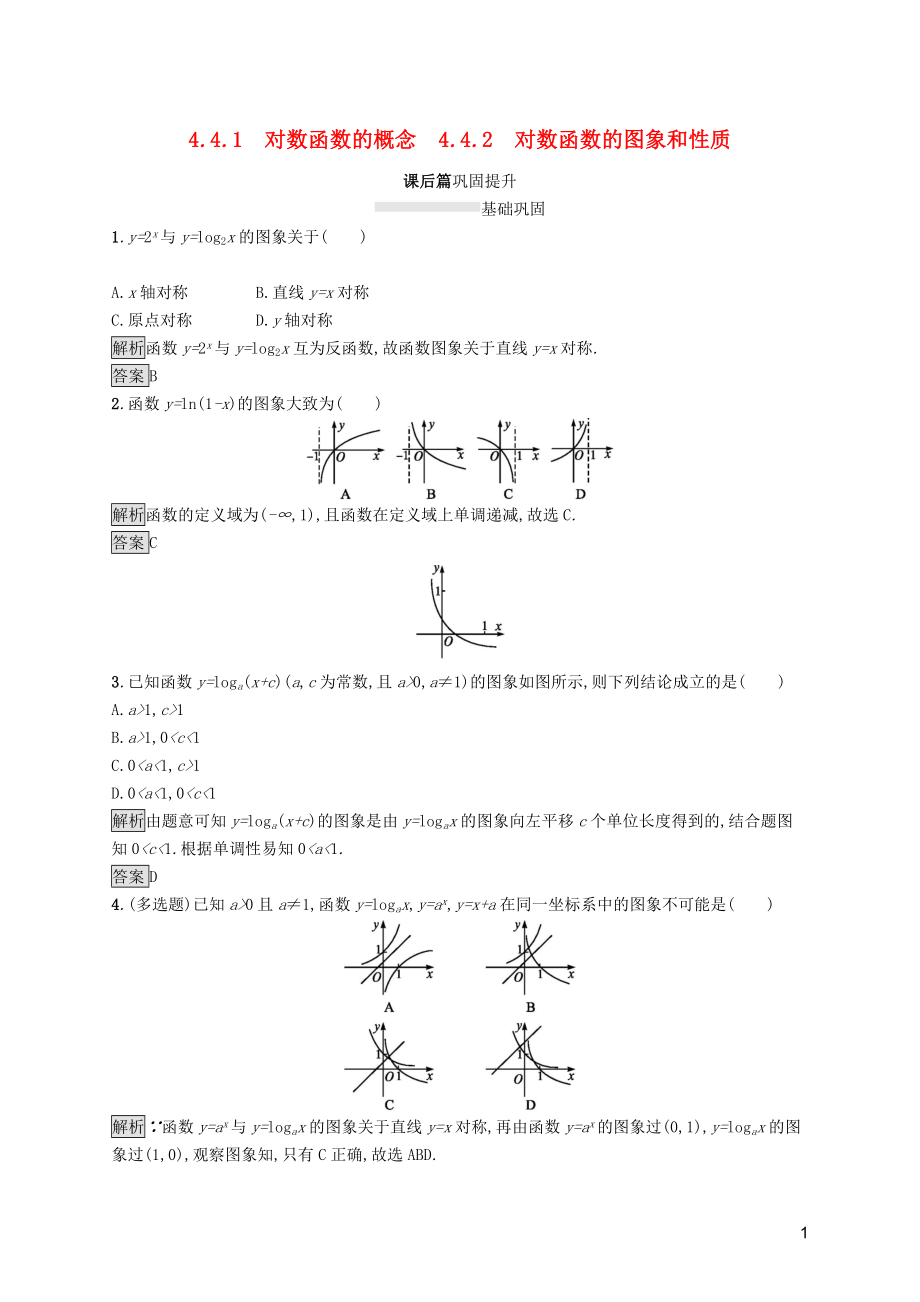
1、4.4.1　對數(shù)函數(shù)的概念　4.4.2　對數(shù)函數(shù)的圖象和性質 課后篇鞏固提升 基礎鞏固 1.y=2x與y=log2x的圖象關于(　　) 　　　　　　　　　　　　　　　　 A.x軸對稱 B.直線y=x對稱 C.原點對稱 D.y軸對稱 解析函數(shù)y=2x與y=log2x互為反函數(shù),故函數(shù)圖象關于直線y=x對稱. 答案B 2.函數(shù)y=ln(1-x)的圖象大致為(　　) 解析函數(shù)的定義域為(-∞,1),且函數(shù)在定義域上單調遞減,故選C. 答案C 3.已知函數(shù)y=loga(x+c)(a,c為常數(shù),且a>0,a≠1)的圖象如圖所示,則下列結論成立的是(　　) A.a>1,c

2、>1 B.a>1,01 D.00且a≠1,函數(shù)y=logax,y=ax,y=x+a在同一坐標系中的圖象不可能是(　　) 解析∵函數(shù)y=ax與y=logax的圖象關于直線y=x對稱,再由函數(shù)y=ax的圖象過(0,1),y=logax的圖象過(1,0),觀察圖象知,只有C正確,故選ABD. 答案ABD 5.已知a=2-13,b=log213,c=log1

3、213,則(　　) A.a>b>c B.a>c>b C.c>b>a D.c>a>b 解析∵0log1212=1,∴c>a>b.故選D. 答案D 6.將y=2x的圖象先　　　　　,再作關于直線y=x對稱的圖象,可得到函數(shù)y=log2(x+1)的圖象(　　)? A.先向上平移一個單位長度 B.先向右平移一個單位長度 C.先向左平移一個單位長度 D.先向下平移一個單位長度 解析本題是關于圖象的平移變換和對稱變換,可求出解析式或利用幾何圖形直觀推斷. 答案D 7.若對數(shù)函數(shù)f(x)的圖象經過點P(8

4、,3),則f12=　　　　　.? 解析設f(x)=logax(a>0,a≠1),則loga8=3, ∴a3=8,∴a=2. ∴f(x)=log2x,故f12=log212=-1. 答案-1 8.已知函數(shù)f(x)=log2x,x>0,3x,x≤0,直線y=a與函數(shù)f(x)的圖象恒有兩個不同的交點,則a的取值范圍是　　　　　.? 解析函數(shù)f(x)的圖象如圖所示,要使直線y=a與f(x)的圖象有兩個不同的交點,則0

5、x在x軸下方的圖象關于x軸對稱翻折到x軸上方(原來在x軸上方的圖象不變),得函數(shù)y=|log2x|的圖象,如圖乙;然后將y=|log2x|的圖象向上平移2個單位長度,得函數(shù)y=|log2x|+2的圖象,如圖丙.由圖丙得函數(shù)y=|log2x|+2的單調遞增區(qū)間是[1,+∞),單調遞減區(qū)間是(0,1),值域是[2,+∞). 10.已知對數(shù)函數(shù)y=f(x)的圖象經過點P(9,2). (1)求y=f(x)的解析式; (2)若x∈(0,1),求f(x)的取值范圍. (3)若函數(shù)y=g(x)的圖象與函數(shù)y=f(x)的圖象關于x軸對稱,求y=g(x)的解析式. 解(1)設f(x)=logax(

6、a>0,且a≠1). 由題意,f(9)=loga9=2,故a2=9, 解得a=3或a=-3. 又因為a>0,所以a=3.故f(x)=log3x. (2)因為3>1,所以當x∈(0,1)時,f(x)<0, 即f(x)的取值范圍為(-∞,0). (3)因為函數(shù)y=g(x)的圖象與函數(shù)y=log3x的圖象關于x軸對稱,所以g(x)=log13x. 能力提升 1.函數(shù)y=loga(x+2)+1(a>0,且a≠1)的圖象過定點(　　) A.(1,2) B.(2,1) C.(-2,1) D.(-1,1) 解析令x+2=1,得x=-1,此時y=1. 答案D 2.若函數(shù)f(x)=log

7、2x的反函數(shù)為y=g(x),且g(a)=14,則a=(　　) A.2 B.-2 C.12 D.-12 解析由題意,得g(x)=2x. ∵g(a)=14,∴2a=14,∴a=-2. 答案B 3.若函數(shù)f(x)=log2(x2-ax-3a)在區(qū)間(-∞,-2]上是減函數(shù),則實數(shù)a的取值范圍是(　　) A.(-∞,4) B.(-4,4] C.(-∞,4)∪[2,+∞) D.[-4,4) 解析令t(x)=x2-ax-3a,則由函數(shù)f(x)=log2t在區(qū)間(-∞,-2]上是減函數(shù),可得函數(shù)t(x)在區(qū)間(-∞,-2]上是減函數(shù),且t(-2)>0,所以有-4≤a<4,故選D. 答案D

8、 4.已知a=log23.6,b=log43.2,c=log43.6,則a,b,c的大小關系為　　　　　.? 解析∵a=log43.6log42=2log43.6=log43.62,又函數(shù)y=log4x在區(qū)間(0,+∞)上是增函數(shù),3.62>3.6>3.2, ∴l(xiāng)og43.62>log43.6>log43.2,∴a>c>b. 答案a>c>b 5.已知a>0且a≠1,則函數(shù)y=ax與y=loga(-x)在同一直角坐標系中的圖象只能是下圖中的　　　　　(填序號).? 解析(方法一)首先,曲線y=ax位于x軸上方,y=loga(-x)位于y軸左側,從而排除①③.其次,從單調性考慮,

9、y=ax與y=loga(-x)的增減性正好相反,又可排除④.故只有②滿足條件. (方法二)若01,則曲線y=ax上升且過點(0,1),而曲線y=loga(-x)下降且過點(-1,0),只有②滿足條件. (方法三)如果注意到y(tǒng)=loga(-x)的圖象關于y軸的對稱圖象為y=logax的圖象,又y=logax與y=ax互為反函數(shù)(兩者圖象關于直線y=x對稱),則可直接選②. 答案② 6.已知函數(shù)f(x)是定義在R上的奇函數(shù),若當x∈(0,+∞)時,f(x)=l

10、g x,則滿足f(x)>0的x的取值范圍是　　　　　　　　　　.? 解析由已知條件可得函數(shù)f(x)的解析式為 f(x)=lgx,x>0,0,x=0,-lg(-x),x<0,其圖象如圖所示. 由函數(shù)圖象可得不等式f(x)>0時,x的取值范圍為(-1,0)∪(1,+∞). 答案(-1,0)∪(1,+∞) 7.設函數(shù)f(x)=ln(ax2+2x+a)的定義域為M. (1)若1?M,2∈M,求實數(shù)a的取值范圍; (2)若M=R,求實數(shù)a的取值范圍. 解(1)由題意M={x|ax2+2x+a>0}. 由1?M,2∈M可得a×12+2×1+a≤0,a×22+2×2+a>0, 化簡得

11、2a+2≤0,5a+4>0,解得-450恒成立. 當a=0時,不等式可化為2x>0,解得x>0,顯然不合題意; 當a≠0時,由二次函數(shù)的圖象可知Δ=22-4×a×a<0,且a>0,即4-4a2<0,a>0,化簡得a2>1,a>0,解得a>1. 所以a的取值范圍為(1,+∞). 8.已知函數(shù)f(x)=log21+axx-1(a為常數(shù))是奇函數(shù). (1)求a的值與函數(shù)f(x)的定義域; (2)若當x∈(1,+∞)時,f(x)+log2(x-1)>m恒成立,求實數(shù)m的取值范圍. 解(1)∵函數(shù)f(x)=log21+axx-1是奇函數(shù), ∴f(-x)=-f(x). ∴l(xiāng)og21-ax-x-1=-log21+axx-1. 即log2ax-1x+1=log2x-11+ax,∴a=1. 令1+xx-1>0,解得x<-1或x>1. 所以函數(shù)的定義域為{x|x<-1或x>1}. (2)f(x)+log2(x-1)=log2(1+x), 當x>1時,x+1>2,∴l(xiāng)og2(1+x)>log22=1. ∵x∈(1,+∞),f(x)+log2(x-1)>m恒成立, ∴m≤1.故m的取值范圍是(-∞,1]. 6