三年模擬一年創(chuàng)新高考數(shù)學(xué)復(fù)習(xí) 第八章 第二節(jié) 空間幾何體的表面積和體積 理全國(guó)通用

《三年模擬一年創(chuàng)新高考數(shù)學(xué)復(fù)習(xí) 第八章 第二節(jié) 空間幾何體的表面積和體積 理全國(guó)通用》由會(huì)員分享，可在線閱讀，更多相關(guān)《三年模擬一年創(chuàng)新高考數(shù)學(xué)復(fù)習(xí) 第八章 第二節(jié) 空間幾何體的表面積和體積 理全國(guó)通用（5頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

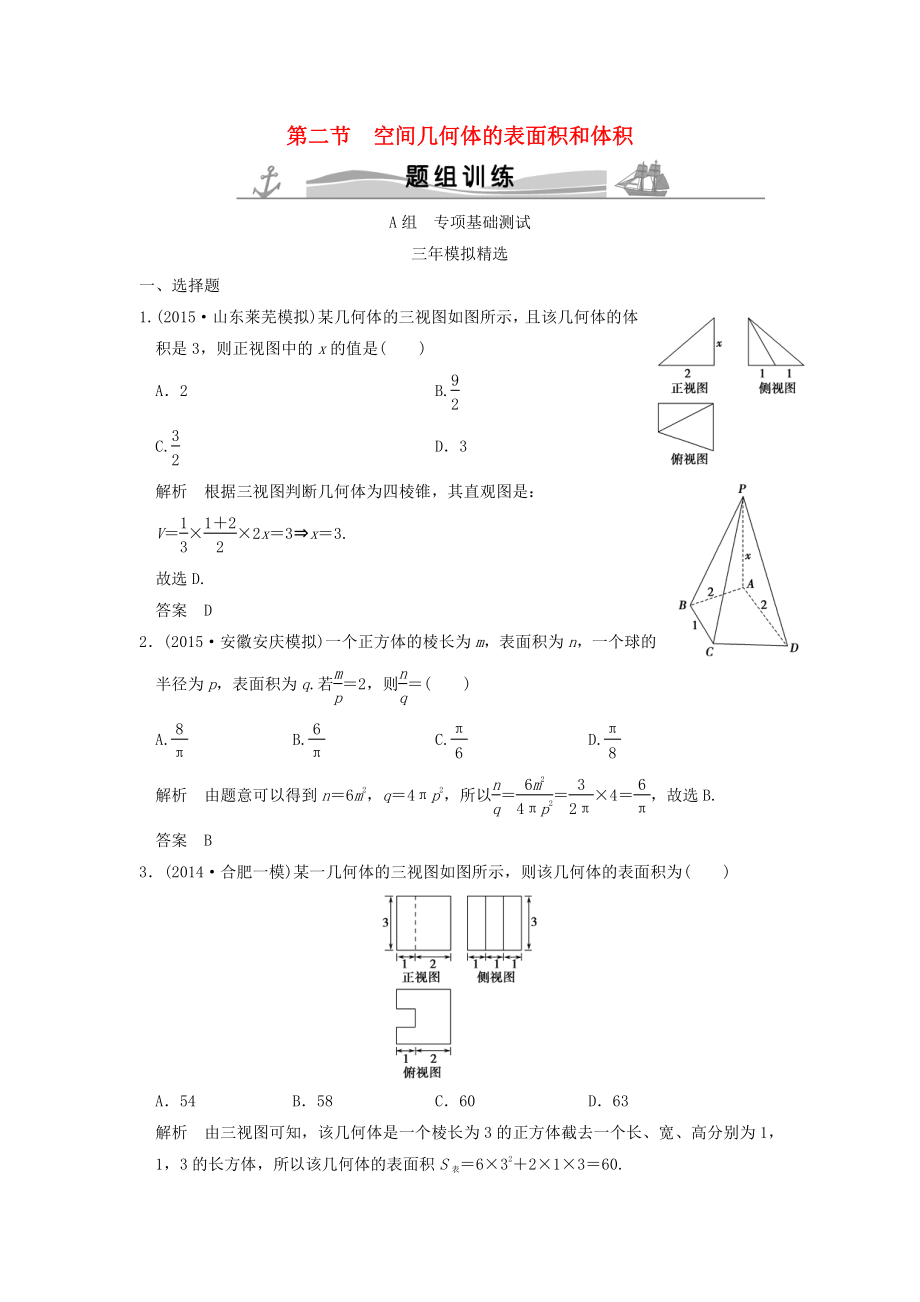
1、第二節(jié)第二節(jié)空間幾何體的表面積和體積空間幾何體的表面積和體積A 組專項(xiàng)基礎(chǔ)測(cè)試三年模擬精選一、選擇題1.(2015山東萊蕪模擬)某幾何體的三視圖如圖所示， 且該幾何體的體積是 3，則正視圖中的x的值是()A2B.92C.32D3解析根據(jù)三視圖判斷幾何體為四棱錐，其直觀圖是：V131222x3x3.故選 D.答案D2(2015安徽安慶模擬)一個(gè)正方體的棱長(zhǎng)為m，表面積為n，一個(gè)球的半徑為p，表面積為q.若mp2，則nq()A.8B.6C.6D.8解析由題意可以得到n6m2，q4p2，所以nq6m24p23246，故選 B.答案B3(2014合肥一模)某一幾何體的三視圖如圖所示，則該幾何體的表面積

2、為()A54B58C60D63解析由三視圖可知，該幾何體是一個(gè)棱長(zhǎng)為 3 的正方體截去一個(gè)長(zhǎng)、寬、高分別為 1，1，3 的長(zhǎng)方體，所以該幾何體的表面積S表63221360.答案C4(2014浙江寧波質(zhì)檢)某幾何體的三視圖如圖所示，它的體積為()A72B48C30D24解析由三視圖可知，該幾何體是半個(gè)球體和一個(gè)倒立圓錐體的組合體，球的半徑為 3，圓錐的底面半徑為 3，高為 4，則根據(jù)體積公式可得幾何體的體積為 30，故選 C.答案C二、填空題5(2014山東德州一模)圓柱形容器的內(nèi)壁底半徑是 10 cm，有一個(gè)實(shí)心鐵球浸沒(méi)于容器的水中， 若取出這個(gè)鐵球， 測(cè)得容器的水面下降了53cm， 則這個(gè)鐵

3、球的表面積為_ cm2.解析設(shè)實(shí)心鐵球的半徑為R，則43R310253，得R5 cm，故這個(gè)鐵球的表面積為S4R2100(cm2)答案100一年創(chuàng)新演練6已知某幾何體的三視圖如圖所示，其中，正視圖、側(cè)視圖均是由三角形與半圓構(gòu)成的，俯視圖由圓與內(nèi)接三角形構(gòu)成，根據(jù)圖中的數(shù)據(jù)可得此幾何體的體積為()A.2316B.4316C.2616D.2312解析據(jù)三視圖可知， 該幾何體是一個(gè)半球(下部)與一個(gè)四面體(上部)的組合體，其直觀圖如圖所示，其中BA，BC，BP兩兩垂直，且BABCBP1，(半)球的直徑長(zhǎng)為AC 2，該幾何體的體積為VV半球VPABC1243AC231312BABCPB2616.答案C

4、B 組專項(xiàng)提升測(cè)試三年模擬精選一、選擇題7.(2015湖北七州模擬)某個(gè)幾何體的三視圖如圖所示(其中正視圖中的圓弧是半徑為 2 的半圓)，則該幾何體的表面積為()A9224B8224C9214D8214解析該幾何體是個(gè)半圓柱與長(zhǎng)方體的組合體，直觀圖如圖，表面積為S5424424525229214.答案C8.(2014山東濰坊一中月考)四棱錐PABCD的三視圖如圖所示，四棱錐PABCD的五個(gè)頂點(diǎn)都在一個(gè)球面上，E，F(xiàn)分別是棱AB，CD的中點(diǎn)，直線EF被球面所截得的線段長(zhǎng)為 2 2，則該球的表面積為()A12B24C36D48解析將三視圖還原為直觀圖如圖， 可得四棱錐PABCD的五個(gè)頂點(diǎn)位于同一個(gè)

5、正方體的頂點(diǎn)處，且與該正方體內(nèi)接于同一個(gè)球，且該正方體的棱長(zhǎng)為a.設(shè)外接球的球心為O，則O也是正方體的中心，設(shè)EF的中點(diǎn)為G，連接OG，OA，AG.根據(jù)題意，直線EF被球面所截得的線段長(zhǎng)為 2 2，即正方體的面對(duì)角線長(zhǎng)也是 2 2，可得AG 222a，所以正方體的棱長(zhǎng)a2，在 RtOGA中，OG12a1，AO 3，即四棱錐PABCD的外接球半徑R 3，從而得外接球表面積為 4R212，故選 A.答案A二、填空題9(2014山東聊城 4 月)用 6 根木棒圍成一個(gè)棱錐，已知其中有兩根的長(zhǎng)度為 3 cm 和 2cm，其余四根的長(zhǎng)度均為 1 cm，則這樣的三棱錐的體積為_cm3.解析由題意知該幾何體

6、如圖所示，SASBSCBC1，AB 2，AC 3，則ABC90，取AC的中點(diǎn)O，連接SO、OB，則SOAC，所以SOSA2AO212，OB12AC32，又SB1，所以SO2OB2SB2，所以SOB90，又SOAC，所以SO底面ABC，故所求三棱錐的體積V132212212.答案212三、解答題10.(2014陽(yáng)泉月考)已知某幾何體的俯視圖是如右圖所示的矩形，正視圖(或稱主視圖)是一個(gè)底邊長(zhǎng)為 8，高為 4 的等腰三角形，側(cè)視圖(或稱左視圖)是一個(gè)底邊長(zhǎng)為 6、高為 4 的等腰三角形(1)求該幾何體的體積V；(2)求該幾何體的側(cè)面積S.解由題設(shè)可知，幾何體是一個(gè)高為 4 的四棱錐，其底面是長(zhǎng)、寬

7、分別為8 和 6 的矩形，正側(cè)面及其相對(duì)側(cè)面均為底邊長(zhǎng)為 8，高為h1的等腰三角形，左、右側(cè)面均為底邊長(zhǎng)為 6，高為h2的等腰三角形，如圖所示(1)幾何體的體積為：V13S矩形h1368464.(2)正側(cè)面及相對(duì)側(cè)面底邊上的高為h1 42325.左、右側(cè)面的底邊上的高為h2 42424 2.故幾何體的側(cè)面面積為：S2(12851264 2)4024 2.11.(2014煙臺(tái)調(diào)研)正三棱錐的高為 1，底面邊長(zhǎng)為 2 6，內(nèi)有一個(gè)球與它的四個(gè)面都相切(如圖)求：(1)這個(gè)正三棱錐的表面積；(2)這個(gè)正三棱錐內(nèi)切球的表面積與體積解(1)底面正三角形中心到一邊的距離為13322 6 2，則正棱錐側(cè)面的

8、斜高為 12（ 2）2 3.S側(cè)3122 6 39 2.S表S側(cè)S底9 21232(2 6)29 26 3.(2)設(shè)正三棱錐PABC的內(nèi)切球球心為O，連接OP，OA，OB，OC，而O點(diǎn)到三棱錐的四個(gè)面的距離都為球的半徑r.VPABCVOPABVOPBCVOPACVOABC13S側(cè)r13SABCr13S表r(3 22 3)r.又VPABC131232(2 6)212 3，(3 22 3)r2 3，得r2 33 22 32 3（3 22 3）1812 62.S內(nèi)切球4( 62)2(4016 6).V內(nèi)切球43( 62)383(9 622).一年創(chuàng)新演練12 如圖所示， 在邊長(zhǎng)為 5 2的正方形ABCD中， 以A為圓心畫一個(gè)扇形，以O(shè)為圓心畫一個(gè)圓，M，N，K為切點(diǎn)，以扇形為圓錐的側(cè)面，以圓O為圓錐底面，圍成一個(gè)圓錐，求圓錐的表面積與體積解設(shè)圓錐的母線長(zhǎng)為l，底面半徑為r，高為h，由已知條件得lr 2r（5 2） 2，2rl2，解得r 2，l4 2.所以Srlr210，hl2r2 30，V13r2h2 303.