《北師大版八年級(jí)上冊(cè)數(shù)學(xué) 1.1探索勾股定理習(xí)題課（無答案）》由會(huì)員分享，可在線閱讀，更多相關(guān)《北師大版八年級(jí)上冊(cè)數(shù)學(xué) 1.1探索勾股定理習(xí)題課（無答案）（3頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、第2課時(shí) 探索勾股定理（2）
一、典型例題
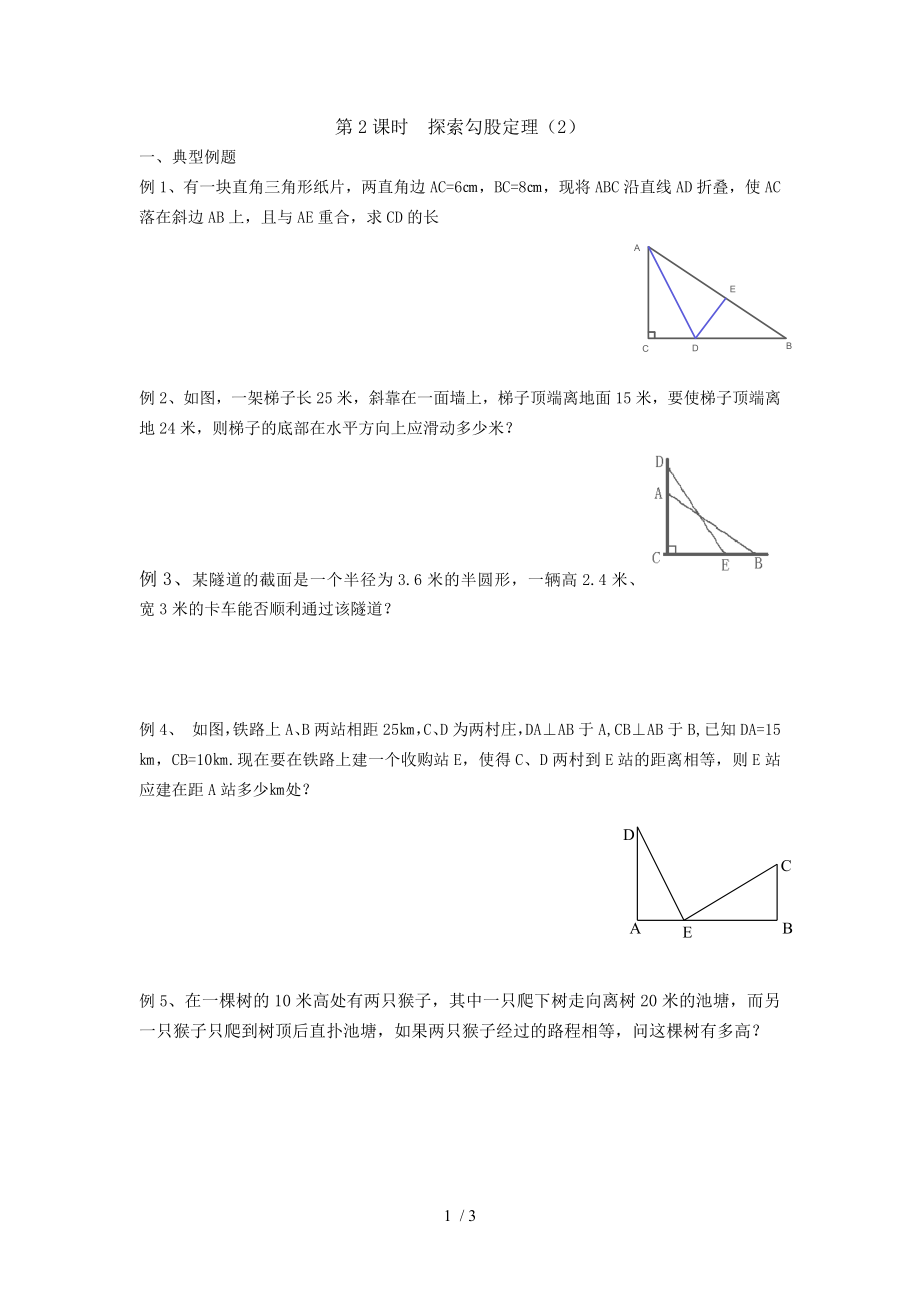
例1、有一塊直角三角形紙片，兩直角邊AC=6㎝，BC=8㎝，現(xiàn)將ABC沿直線AD折疊，使AC落在斜邊AB上，且與AE重合，求CD的長(zhǎng)
例2、如圖，一架梯子長(zhǎng)25米，斜靠在一面墻上，梯子頂端離地面15米，要使梯子頂端離地24米，則梯子的底部在水平方向上應(yīng)滑動(dòng)多少米？
例3、某隧道的截面是一個(gè)半徑為3.6米的半圓形，一輛高2.4米、寬3米的卡車能否順利通過該隧道？
例4、 如圖，鐵路上A、B兩站相距25㎞，C、D為兩村莊，DA⊥AB于A,CB⊥AB于B,已知DA=15㎞，CB=10㎞.現(xiàn)在要在
2、鐵路上建一個(gè)收購(gòu)站E，使得C、D兩村到E站的距離相等，則E站應(yīng)建在距A站多少㎞處？
A
D
E
B
C
例5、在一棵樹的10米高處有兩只猴子，其中一只爬下樹走向離樹20米的池塘，而另一只猴子只爬到樹頂后直撲池塘，如果兩只猴子經(jīng)過的路程相等，問這棵樹有多高？
例6、以Rt△ABC三邊為直徑作半圓，這三個(gè)半圓的面積S1、S2、S3之間有什么關(guān)系？說明理由。
二、知識(shí)鞏固
1.等腰直角三角形三邊的平方比為
2.等腰三角形的底邊為10cm，周長(zhǎng)為36cm，則它的面積是
3、 cm2.
3.長(zhǎng)方形的一條對(duì)角線的長(zhǎng)為10cm，一邊長(zhǎng)為6cm，它的面積是
4.RtABC中，，AB=2，則AB2+BC2+CA2= .
5.一個(gè)直角三角形的三邊為三個(gè)連續(xù)偶數(shù)，則它的三邊長(zhǎng)分別為 ．
6. 直角三角形兩直角邊的比為3：4，面積是24，求這個(gè)三角形的周長(zhǎng).
7. 如圖，已知長(zhǎng)方形ABCD沿直線BD折疊，使點(diǎn)C落在C′處，BC′交AD于E，AD=8，AB=4，求DE的長(zhǎng).
8. 在Rt△ABC中，∠C=90°c=25，b=15，求a；
9.如圖，池塘邊有兩點(diǎn)A,B，點(diǎn)C是與BA方向成直角的AC方向上的一點(diǎn)，現(xiàn)測(cè)得CB=60m,AC=20m.求A，B兩點(diǎn)間的距離(結(jié)果取整數(shù)).
第9題圖 第10題圖
10.如圖，在平面直角坐標(biāo)系中有兩點(diǎn)A(5，0)和B(0，4)，求這兩點(diǎn)間的距離.
3 / 3
北師大版八年級(jí)上冊(cè)數(shù)學(xué) 1.1探索勾股定理習(xí)題課（無答案）
