北師大版八年級數(shù)學上冊第四章 4.4.2含一個一次函數(shù)(圖象)的應(yīng)用 同步作業(yè)

《北師大版八年級數(shù)學上冊第四章 4.4.2含一個一次函數(shù)(圖象)的應(yīng)用 同步作業(yè)》由會員分享，可在線閱讀，更多相關(guān)《北師大版八年級數(shù)學上冊第四章 4.4.2含一個一次函數(shù)(圖象)的應(yīng)用 同步作業(yè)（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

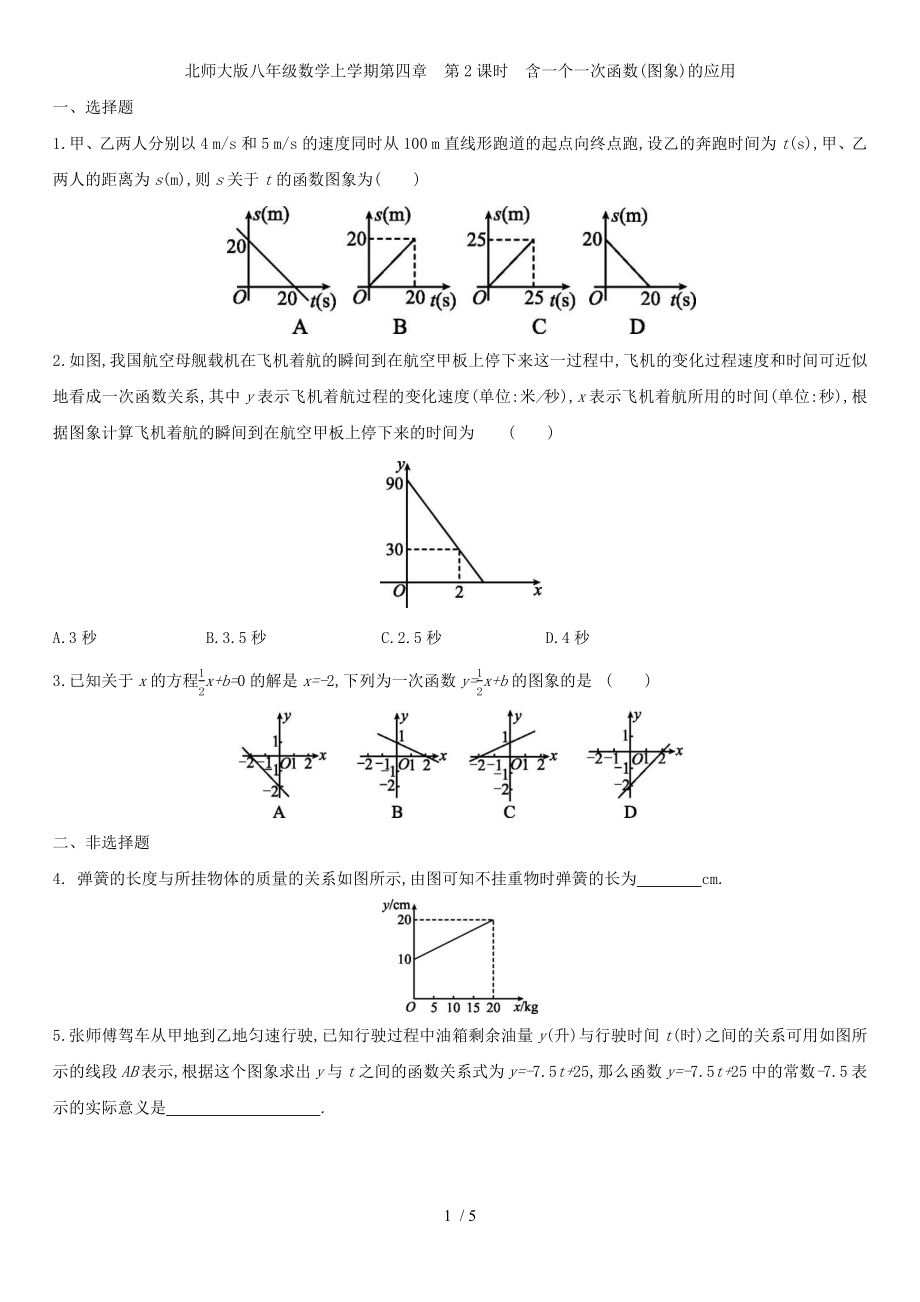
1、北師大版八年級數(shù)學上學期第四章　第2課時　含一個一次函數(shù)(圖象)的應(yīng)用 一、選擇題 1.甲、乙兩人分別以4 m/s和5 m/s的速度同時從100 m直線形跑道的起點向終點跑,設(shè)乙的奔跑時間為t(s),甲、乙兩人的距離為s(m),則s關(guān)于t的函數(shù)圖象為(　　) 2.如圖,我國航空母艦載機在飛機著航的瞬間到在航空甲板上停下來這一過程中,飛機的變化過程速度和時間可近似地看成一次函數(shù)關(guān)系,其中y表示飛機著航過程的變化速度(單位:米/秒),x表示飛機著航所用的時間(單位:秒),根據(jù)圖象計算飛機著航的瞬間到在航空甲板上停下來的時間為 (　　) A.3秒 B.3.5秒 C.2.5秒 D.4秒

2、 3.已知關(guān)于x的方程12x+b=0的解是x=-2,下列為一次函數(shù)y=12x+b的圖象的是 (　　) 二、非選擇題 4. 彈簧的長度與所掛物體的質(zhì)量的關(guān)系如圖所示,由圖可知不掛重物時彈簧的長為　　　　cm.? 5.張師傅駕車從甲地到乙地勻速行駛,已知行駛過程中油箱剩余油量y(升)與行駛時間t(時)之間的關(guān)系可用如圖所示的線段AB表示,根據(jù)這個圖象求出y與t之間的函數(shù)關(guān)系式為y=-7.5t+25,那么函數(shù)y=-7.5t+25中的常數(shù)-7.5表示的實際意義是　 .? 6.某廠家在甲商場銷售一種商品所獲利潤y(單位:元)與銷售數(shù)量x(單位:件)之

3、間的函數(shù)關(guān)系如圖所示,請根據(jù)圖象解決下列問題: (1)求y與x之間的函數(shù)關(guān)系式(不要求寫出自變量的取值范圍); (2)銷售該商品800件時,廠家可獲得的利潤是多少元? 7. 某商場在一樓到二樓之間設(shè)有上下行自動扶梯和步行樓梯.甲、乙兩人從二樓同時下行,甲乘自動扶梯,乙走步行樓梯,甲離一樓地面的高度h(單位:m)與下行時間x(單位:s)之間具有函數(shù)關(guān)系h=-310x+6,乙離一樓地面的高度y(單位:m)與下行時間x(單位:s)之間的函數(shù)關(guān)系如圖所示. (1)求y與x之間的函數(shù)關(guān)系式(不要求寫出自變量的取值范圍); (2)請通過計算說明甲、乙兩人誰先到達一樓地面. 8.

4、一輛汽車在某次行駛過程中,油箱中的剩余油量y(L)與行駛路程x(km)之間是一次函數(shù)關(guān)系,其部分圖象如圖所示. (1)求y關(guān)于x的函數(shù)關(guān)系式(不需要寫出自變量的取值范圍); (2)已知當油箱中的剩余油量為8 L時,該汽車會開始提示加油,在此次行駛過程中,行駛了500 km時,司機發(fā)現(xiàn)離前方最近的加油站有30 km的路程,在開往該加油站的途中,汽車開始提示加油,這時離加油站的路程是多少千米? 9.已知關(guān)于x的方程mx+n=0的解是x=-2,則直線y=mx+n與x軸的交點坐標是　　　　.? 10.如圖,已知直線y=ax+b,則方程ax+b=1的解是x=　　　　.? 11.某食

5、品加工廠需要一批食品包裝盒,供應(yīng)這種包裝盒有兩種方案可供選擇: 方案一:從包裝盒加工廠直接購買,購買所需的費用y1與包裝盒的個數(shù)x之間的函數(shù)關(guān)系如圖①所示. 方案二:租賃機器自己加工,所需費用y2(包括租賃機器的費用和生產(chǎn)包裝盒的費用)與包裝盒的個數(shù)x之間的函數(shù)關(guān)系如圖②所示.根據(jù)圖象回答下列問題: (1)方案一中每個包裝盒的價格是多少元? (2)方案二中租賃機器的費用是多少元?生產(chǎn)一個包裝盒的費用是多少元? (3)請分別求出y1,y2與x之間的函數(shù)關(guān)系式; (4)如果你是決策者,你認為選擇哪種方案更省錢? 參考答案 1.B　[解析] 因為甲、乙兩人分別以4 m/s和5

6、 m/s的速度起跑,所以兩人的速度差為1 m/s, 乙從起點到終點所需時間為20 s,所以乙到達終點時兩人相距20×1=20(m).故選B. 2.A　[解析] 設(shè)y與x之間的函數(shù)表達式為y=kx+b,把(0,90)和(2,30)代入,得b=90,2k+b=30,解得k=-30.所以y=-30x+90,當y=0時,-30x+90=0,解得x=3.故選A. 3.C 二、非選擇題 4.10　[解析] 根據(jù)圖象可以得出當x=0時,y=10.因此,不掛重物時彈簧的長為10 cm. 5.該車每小時耗油7.5升 6.解:(1)設(shè)y=kx.由圖象可知當x=600時,y=4800,將x=600,y

7、=4800代入y=kx,得4800=600k,解得k=8,所以y=8x. (2)當x=800時,y=8×800=6400. 因此,銷售該商品800件時,廠家可獲得的利潤是6400元. 7.解:(1)設(shè)y=kx+b. 將(0,6)代入y=kx+b,可得b=6. 將(15,3)代入y=kx+6,得3=15k+6,解得k=-15,所以y=-15x+6. (2)對于甲:令h=0,則-310x+6=0,解得x=20,對于乙:令y=0,則-15x+6=0,解得x=30. 因為20<30,所以甲比乙先到達一樓地面. 8.解:(1)設(shè)該一次函數(shù)關(guān)系式為y=kx+b. 將(150,45),(0

8、,60)代入y=kx+b,得150k+b=45,b=60, 解得k=-110. 所以該一次函數(shù)關(guān)系式為y=-110x+60. (2)當y=-110x+60=8時,解得x=520. 即行駛520 km時,油箱中的剩余油量為8 L. 500+30-520=10(km). 故當油箱中的剩余油量為8 L時,距離加油站10 km. 所以在開往該加油站的途中,汽車開始提示加油,這時離加油站的路程是10 km. 9.(-2,0)　[解析] 直線y=mx+n中,令y=0,則mx+n=0.因為方程mx+n=0的解為x=-2,所以直線y=mx+n與x軸的交點坐標是(-2,0). 10.4　[解析

9、] 根據(jù)圖象知,當y=1時,x=4,即當ax+b=1時,x=4, 所以方程ax+b=1的解是x=4. 11.[解析] (1)根據(jù)圖①可知購買100個包裝盒共花費500元,據(jù)此可以求出每個包裝盒的價格; (2)根據(jù)圖②可以知道租賃機器花費20000元,根據(jù)圖象所經(jīng)過的點的坐標求出生產(chǎn)一個包裝盒的費用即可; (3)根據(jù)圖象經(jīng)過的點的坐標可求得函數(shù)關(guān)系式; (4)求出當x的值為多少時,兩種方案的費用相同,并在此基礎(chǔ)上分類討論更省錢的方案即可. 解:(1)500÷100=5(元), 所以方案一中每個包裝盒的價格為5元. (2)根據(jù)函數(shù)的圖象可以知道租賃機器的費用為20000元, (3

10、0000-20000)÷4000=2.5(元), 故生產(chǎn)一個包裝盒的費用為2.5元. (3)設(shè)y1與x之間的函數(shù)關(guān)系式為y1=k1x, 由圖象經(jīng)過點(100,500), 得500=100k1, 解得k1=5, 所以y1=5x(x>0,且x為整數(shù)); 設(shè)y2與x之間的函數(shù)關(guān)系式為y2=k2x+b. 由圖象經(jīng)過點(0,20000)和(4000,30000), 可知b=20000, 把(4000,30000)代入y2=k2x+20000,得k2=2.5, 所以y2=2.5x+20000(x>0,且x為整數(shù)). (4)令5x=2.5x+20000,解得x=8000, 所以當x=8000時,兩種方案的費用相同; 當08000時,選擇方案二更省錢. 5 / 5