《2022年高一上學期第二次月考數(shù)學試題 缺答案》由會員分享，可在線閱讀，更多相關《2022年高一上學期第二次月考數(shù)學試題 缺答案（4頁珍藏版）》請在裝配圖網上搜索。
1、2022年高一上學期第二次月考數(shù)學試題 缺答案
一、選擇題：本大題共12小題，每小題5分，共60分. 在每小題給出的四個選項中，只有一項是符合題目要求的．
1．下列函數(shù)中與是同一個函數(shù)的是（ ）
A. B. C. D．
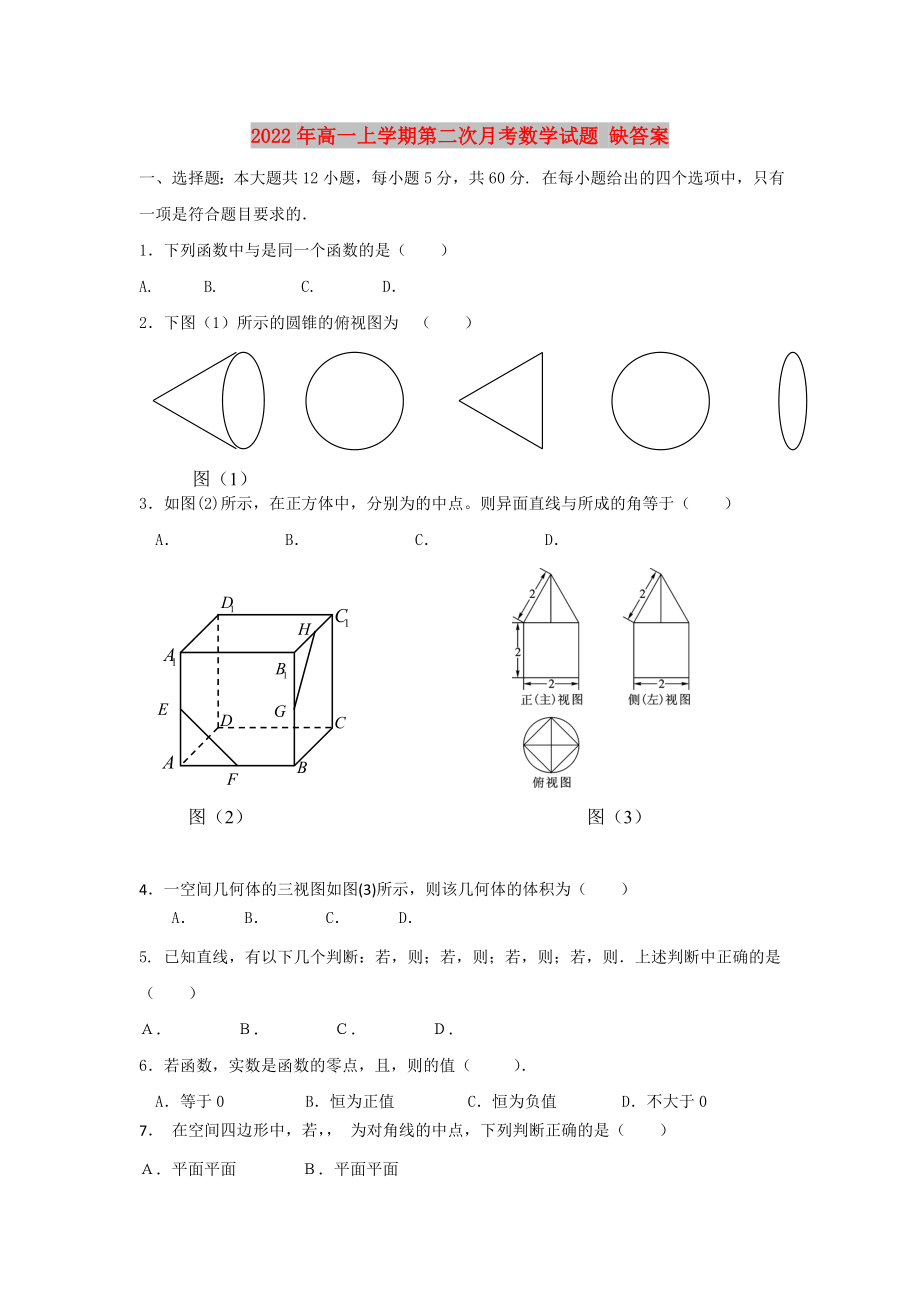
2．下圖（1）所示的圓錐的俯視圖為 （ ）
圖（1）
3．如圖(2)所示，在正方體中，分別為的中點。則異面直線與所成的角等于（ ）
A． B． C． D．
2、
圖（2） 圖（3）
4．一空間幾何體的三視圖如圖(3)所示，則該幾何體的體積為（ ）
A． B． C． D．
5. 已知直線，有以下幾個判斷：若，則；若，則；若，則；若，則．上述判斷中正確的是（ ?。?
Ａ． Ｂ． Ｃ． Ｄ．
6．若函數(shù)，實數(shù)是函數(shù)的零點，且，則的值（ ）．
A．等于0 B．恒為正值 C．恒為負值 D．不大于0
7． 在空間四邊形中，若，， 為對角線的中點，下列判斷正確的是
3、（ ?。?
Ａ．平面平面 Ｂ．平面平面
Ｃ．平面平面 Ｄ．平面平面
8．已知，且，則函數(shù)與函數(shù)的圖像可能是
9．在空間四邊形中，分別是的中點。若，且與所成的角為，則四邊形的面積為 （ ）
、； 、； 、； 、。
10.已知兩個平面垂直，下列命題
一個平面內已知直線必垂直于另一個平面內的任意一條直線．
一個平面內的已知直線必垂直于另一個平面的無數(shù)條直線．
一個平面內的任一條直線必垂直于另一個平面．
過一個平面內任意一點作交線的垂線，則此垂線必垂直于另一個平面．
其中正確的個數(shù)是（ ?。?
A．３ Ｂ．２
4、 Ｃ．１ Ｄ．０
11. 已知函數(shù)若在上單調遞增，則實數(shù)的取值范圍為（ ）
A． B． C． D．
12.已知是定義在上的偶函數(shù)，當時，，則不等式的解集為（ ）
A． B. C. D.
二、填空題：本大題共4小題，每小題5分，共20分．
13．函數(shù)恒過定點，其坐標為 ．
14．半徑為a的球放在墻角，同時與兩墻面和地面相切，那么球心到墻角頂點的距離為________________；
15.一個圓柱和一個圓錐的底面直徑和它們的高都與某一個球的直徑相等，這時圓
5、柱、圓錐、球的體積之比為 ．
M
T
16．是兩個不同的平面，是平面及之外的兩條不同的直線，給出四個論斷：；；；．以其中三個論斷作為條件，余下的一個論斷作為結論，寫出你認為正確的一個命題 ?。?
第Ⅱ卷（滿分70分）
三、解答題
17.(本小題滿分10分)
已知函數(shù)為奇函數(shù).
（1）求的定義域；（2）求的值；（3）求證：當時，.
18. (本小題滿分12分)
已知關于的不等式的解集為．
（1）求集合； （2）若，求函數(shù)的最值．
19. (本小題滿分12分)如圖(4)，在底面是直角梯形的四棱錐S-ABCD中，
6、S
C
A
D
B
(1)求四棱錐S-ABCD的體積;
(2)求證：
(3)求SC與底面ABCD所成角的正切值。
圖（4）
20. (本小題滿分12分)
長方體中，，過，，三點的平面截去長方體的一個角后，得到如圖所示的幾何體，這個幾何體的體積為。
（1）求證：直線∥平面;
（2）求證 ：;
（3）求棱的長.
21.(本小題滿分12分)
設二次函數(shù)在區(qū)間上的最大值，最小值分別為. 集合
（1）若，且，求和的值；
（2）若，且，記，求的最小值.
22.(本小題滿分12分)
如下圖（5），在三棱錐中，分別是的中點， .
（1） 求證：平面； （2） 求異面直線與所成角的余弦值；
A
B
C
圖（5）
（3） 求點到平面的距離。
2022年高一上學期第二次月考數(shù)學試題 缺答案
