《2018屆中考數(shù)學(xué)專(zhuān)項(xiàng)復(fù)習(xí) 軸對(duì)稱(chēng)綜合訓(xùn)練》由會(huì)員分享�����,可在線閱讀,更多相關(guān)《2018屆中考數(shù)學(xué)專(zhuān)項(xiàng)復(fù)習(xí) 軸對(duì)稱(chēng)綜合訓(xùn)練(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1、
軸對(duì)稱(chēng)
1.下列軸對(duì)稱(chēng)圖形中���,只用一把無(wú)刻度的直尺不能畫(huà)出對(duì)稱(chēng)軸的是( )
A.菱形 B.矩形 C.等腰梯形 D.正五邊形
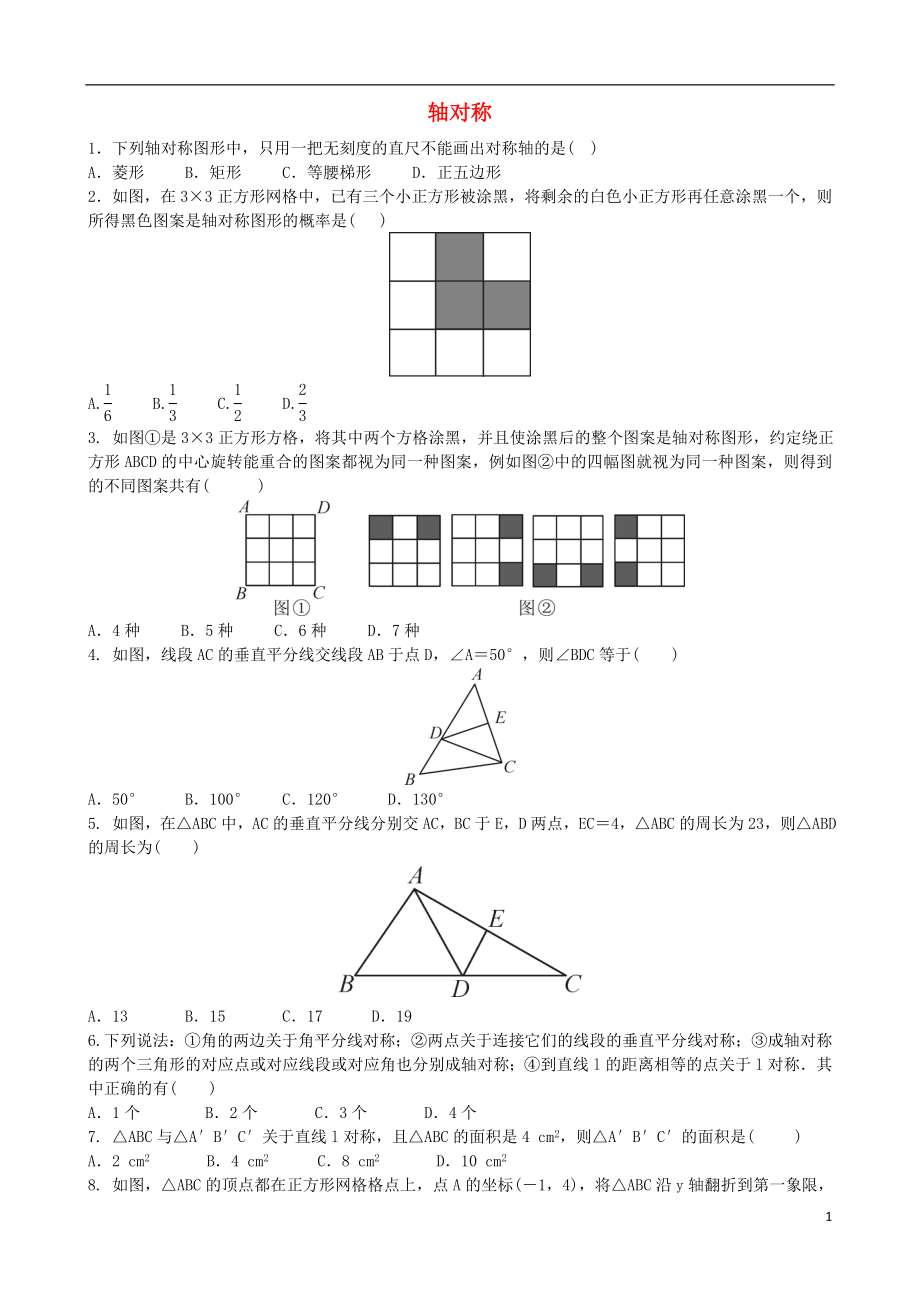
2.如圖���,在3×3正方形網(wǎng)格中,已有三個(gè)小正方形被涂黑����,將剩余的白色小正方形再任意涂黑一個(gè),則所得黑色圖案是軸對(duì)稱(chēng)圖形的概率是( )
A. B. C. D.
3. 如圖①是3×3正方形方格����,將其中兩個(gè)方格涂黑,并且使涂黑后的整個(gè)圖案是軸對(duì)稱(chēng)圖形�����,約定繞正方形ABCD的中心旋轉(zhuǎn)能重合的圖案都視為同一種圖案���,例如圖②中的四幅圖就視為同一種圖案����,則得到的不同圖案共有( )
A.4種
2、B.5種 C.6種 D.7種
4. 如圖�,線段AC的垂直平分線交線段AB于點(diǎn)D,∠A=50°�,則∠BDC等于( )
A.50° B.100° C.120° D.130°
5. 如圖,在△ABC中��,AC的垂直平分線分別交AC���,BC于E����,D兩點(diǎn)���,EC=4,△ABC的周長(zhǎng)為23�����,則△ABD的周長(zhǎng)為( )
A.13 B.15 C.17 D.19
6. 下列說(shuō)法:①角的兩邊關(guān)于角平分線對(duì)稱(chēng)����;②兩點(diǎn)關(guān)于連接它們的線段的垂直平分線對(duì)稱(chēng);③成軸對(duì)稱(chēng)的兩個(gè)三角形的對(duì)應(yīng)點(diǎn)或?qū)?yīng)線段或?qū)?yīng)角也分別成軸對(duì)稱(chēng)�����;④到
3、直線l的距離相等的點(diǎn)關(guān)于l對(duì)稱(chēng).其中正確的有( )
A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè)
7. △ABC與△A′B′C′關(guān)于直線l對(duì)稱(chēng)�����,且△ABC的面積是4 cm2��,則△A′B′C′的面積是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.10 cm2
8. 如圖���,△ABC的頂點(diǎn)都在正方形網(wǎng)格格點(diǎn)上���,點(diǎn)A的坐標(biāo)(-1,4)����,將△ABC沿y軸翻折到第一象限,則點(diǎn)C的對(duì)應(yīng)點(diǎn)C′的坐標(biāo)是( )
A.(3�,1) B.(-3,-1) C.(1�����,-3) D.(3���,-1)
4���、
9. 在平面直角坐標(biāo)系中��,將點(diǎn)A(1����,2)的橫坐標(biāo)乘以-1�,縱坐標(biāo)不變,得到點(diǎn)A′���,則點(diǎn)A和點(diǎn)A′的關(guān)系是( )
A.關(guān)于x軸對(duì)稱(chēng) B.關(guān)于y軸對(duì)稱(chēng)
C.關(guān)于原點(diǎn)對(duì)稱(chēng) D.將點(diǎn)A向x軸負(fù)方向平移一個(gè)單位得到A′
10. 如圖�,直線l是一條河�,P,Q是兩個(gè)村莊�,欲在l上的某處修建一個(gè)水泵站���,分別向P����,Q兩地供水����,現(xiàn)有如下四種鋪設(shè)方案���,圖中實(shí)線表示鋪設(shè)的管道,則所需管道最短的是( )
11. 如圖�,OE是∠AOB的平分線,BD⊥OA于點(diǎn)D���,AC⊥BO于點(diǎn)C���,則關(guān)于直線OE對(duì)稱(chēng)的三角形共有 對(duì).
12. 如圖,在
5�����、△ABC中�,BC邊上的垂直平分線DE交邊BC于點(diǎn)D,交邊AB于點(diǎn)E.若△EDC的周長(zhǎng)為24����,△ABC與四邊形AEDC的周長(zhǎng)之差為12,則線段DE的長(zhǎng)為 .
13. 點(diǎn)P(1���,2)關(guān)于直線y=1對(duì)稱(chēng)的點(diǎn)的坐標(biāo)是 .
關(guān)于直線x=2對(duì)稱(chēng)的點(diǎn)的坐標(biāo)是 .
14. 如圖�,已知E為∠AOB的平分線上一點(diǎn),EC⊥OA�,ED⊥OB,垂足分別為C�����,D.求證:OE垂直平分CD.
參考答案:
1—10 BDCBB CBABD
11. 4
12. 6
13. (1����,0) (3,2)
14. 解:∵E在∠AOB的平分線上�,ED⊥OB于點(diǎn)D,EC⊥OA于點(diǎn)C��,∴ED=EC.在Rt△EDO和Rt△ECO中�����,ED=EC��,OE=OE����,∴Rt△EDO≌Rt△ECO,∴OD=OC�����,∴O��,E都在CD的垂直平分線上���,∴OE垂直平分CD
3
 2018屆中考數(shù)學(xué)專(zhuān)項(xiàng)復(fù)習(xí) 軸對(duì)稱(chēng)綜合訓(xùn)練
2018屆中考數(shù)學(xué)專(zhuān)項(xiàng)復(fù)習(xí) 軸對(duì)稱(chēng)綜合訓(xùn)練