《2018年秋高中數(shù)學(xué) 第二章 數(shù)列 階段復(fù)習(xí)課 第2課 數(shù)列學(xué)案 新人教A版必修5》由會(huì)員分享����,可在線閱讀�����,更多相關(guān)《2018年秋高中數(shù)學(xué) 第二章 數(shù)列 階段復(fù)習(xí)課 第2課 數(shù)列學(xué)案 新人教A版必修5(8頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
1���、
第二課 數(shù)列
[核心速填]
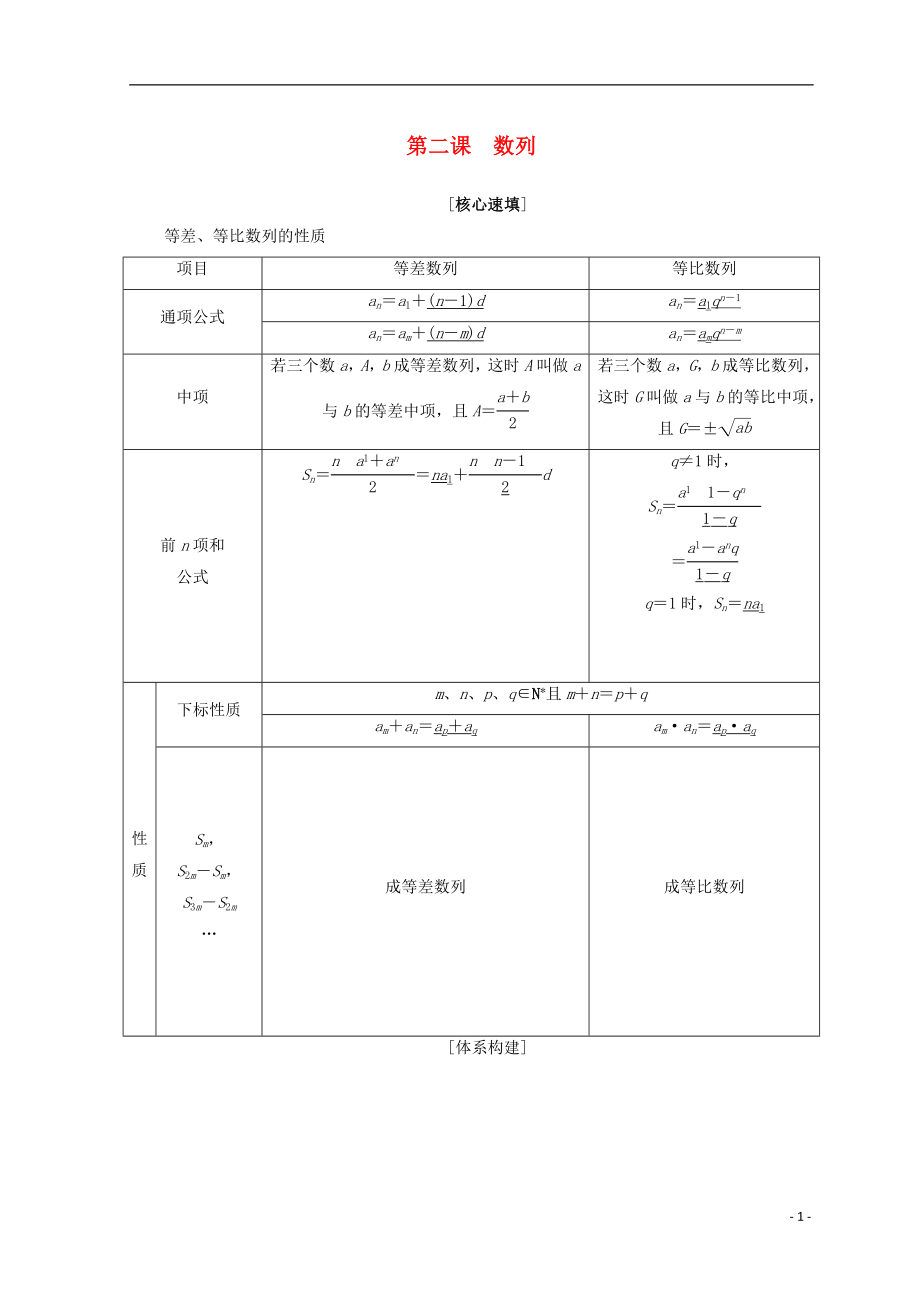
等差��、等比數(shù)列的性質(zhì)
項(xiàng)目
等差數(shù)列
等比數(shù)列
通項(xiàng)公式
an=a1+(n-1)d
an=a1qn-1
an=am+(n-m)d
an=amqn-m
中項(xiàng)
若三個(gè)數(shù)a���,A,b成等差數(shù)列��,這時(shí)A叫做a與b的等差中項(xiàng)��,且A=
若三個(gè)數(shù)a��,G,b成等比數(shù)列�����,這時(shí)G叫做a與b的等比中項(xiàng),且G=±
前n項(xiàng)和
公式
Sn==na1+d
q≠1時(shí)����,
Sn=
=
q=1時(shí)��,Sn=na1
性
質(zhì)
下標(biāo)性質(zhì)
m���、n、p�、q∈N*且m+n=p+q
am+an=ap+aq
am·an=ap·aq
Sm���,
S2m-Sm����,
S3m-
2�����、S2m
…
成等差數(shù)列
成等比數(shù)列
[體系構(gòu)建]
[題型探究]
等差(比)數(shù)列的基本運(yùn)算
等比數(shù)列{an}中��,已知a1=2����,a4=16.
(1)求數(shù)列{an}的通項(xiàng)公式��;
(2)若a3,a5分別為等差數(shù)列{bn}的第3項(xiàng)和第5項(xiàng)�,試求數(shù)列{bn}的通項(xiàng)公式及前n項(xiàng)和Sn.
[解] (1)設(shè){an}的公比為q����,
由已知得16=2q3,
解得q=2�����,∴an=2×2n-1=2n.
(2)由(1)得a3=8��,a5=32�����,
則b3=8,b5=32.
設(shè){bn}的公差為d�����,則有
解得
所以bn=-16+12(n-1)=12n-28.
所以數(shù)列{bn}的前n項(xiàng)和
3��、
Sn==6n2-22n.
[規(guī)律方法]
在等差數(shù)列和等比數(shù)列的通項(xiàng)公式an與前n項(xiàng)和公式Sn中��,共涉及五個(gè)量:a1�,an��,n�����,d(或q)�,Sn�,其中a1和d(或q)為基本量��,“知三求二”是指將已知條件轉(zhuǎn)換成關(guān)于a1�,d(q)����,an����,Sn��,n的方程組���,利用方程的思想求出需要的量�����,當(dāng)然在求解中若能運(yùn)用等差(比)數(shù)列的性質(zhì)會(huì)更好����,這樣可以化繁為簡(jiǎn)�,減少運(yùn)算量��,同時(shí)還要注意整體代入思想方法的運(yùn)用.
[跟蹤訓(xùn)練]
1.已知等差數(shù)列{an}的公差d=1����,前n項(xiàng)和為Sn.
(1)若1���,a1�����,a3成等比數(shù)列���,求a1�����;
(2)若S5>a1a9��,求a1的取值范圍.
【導(dǎo)學(xué)號(hào):91432240】
4�、
[解] (1)因?yàn)閿?shù)列{an}的公差d=1���,且1,a1��,a3成等比數(shù)列�,所以a=1×(a1+2)���,
即a-a1-2=0��,解得a1=-1或a1=2.
(2)因?yàn)閿?shù)列{an}的公差d=1����,且S5>a1a9���,
所以5a1+10>a+8a1,
即a+3a1-10<0�,解得-5
5��、當(dāng)n≥2時(shí)���,an=Sn-Sn-1=3+2n-(3+2n-1)=2n-1,
當(dāng)n=1時(shí)�����,a1=S1=5不適合上式.
∴an=
(2)∵Sn=3an+1�, ①
∴n≥2時(shí)�,Sn-1=3an. ②
①-②得Sn-Sn-1=3an+1-3an�,
∴3an+1=4an����,
∴=,又a2=S1=a1=.
∴n≥2時(shí)����,an=·n-2����,不適合n=1.
∴an=
[規(guī)律方法] 數(shù)列通項(xiàng)公式的求法
(1)定義法
6�����、,即直接利用等差數(shù)列或等比數(shù)列的定義求通項(xiàng)的方法叫定義法�����,這種方法適用于已知數(shù)列類型的題目.
(2)已知Sn求an.若已知數(shù)列的前n項(xiàng)和Sn與an的關(guān)系�,求數(shù)列{an}的通項(xiàng)an可用公式an=求解.
(3))累加或累乘法,形如an-an-1=f(n)(n≥2)的遞推式�����,可用累加法求通項(xiàng)公式�����;形如=f(n)(n≥2)的遞推式,可用累乘法求通項(xiàng)公式.
[跟蹤訓(xùn)練]
2.設(shè)數(shù)列{an}是首項(xiàng)為1的正項(xiàng)數(shù)列��,且an+1-an+an+1·an=0(n∈N*)��,求{an}的通項(xiàng)公式.
【導(dǎo)學(xué)號(hào):91432241】
[解] ∵an+1-an+an+1·an=0�����,
∴-=1.又=1��,
∴是首
7、項(xiàng)為1�����,公差為1的等差數(shù)列.
故=n.
∴an=.
等差(比)數(shù)列的判定
數(shù)列{an}的前n項(xiàng)和為Sn���,a1=1,Sn+1=4an+2(n∈N*).
(1)設(shè)bn=an+1-2an���,求證:{bn}是等比數(shù)列.
(2)設(shè)cn=����,求證:{cn}是等差數(shù)列.
思路探究:分別利用等比數(shù)列與等差數(shù)列的定義進(jìn)行證明.
[證明] (1)an+2=Sn+2-Sn+1=4an+1+2-4an-2
=4an+1-4an.
====2.
因?yàn)镾2=a1+a2=4a1+2�����,所以a2=5.
所以b1=a2-2a1=3.
所以數(shù)列{bn}是首項(xiàng)為3���,公比為2的等比數(shù)列.
(2)由(1)知
8�、bn=3·2n-1=an+1-2an���,
所以-=3.
所以cn+1-cn=3,且c1==2��,
所以數(shù)列{cn}是等差數(shù)列���,公差為3���,首項(xiàng)為2.
[規(guī)律方法] 等差數(shù)列�、等比數(shù)列的判斷方法
(1)定義法:an+1-an=d(常數(shù))?{an}是等差數(shù)列��;(q為常數(shù)����,q≠0)?{an}是等比數(shù)列.
(2)中項(xiàng)公式法:2an+1=an+an+2?{an}是等差數(shù)列;是等比數(shù)列.
(3)通項(xiàng)公式法:an=kn+b(k,b是常數(shù))?{an}是等差數(shù)列��;an=c·qn(c���,q為非零常數(shù))?{an}是等比數(shù)列.
(4)前n項(xiàng)和公式法:Sn=An2+Bn(A,B為常數(shù)�,n∈N*)?{an}是等差
9����、數(shù)列��;Sn=Aqn-A(A�,q為常數(shù),且A≠0��,q≠0�����,q≠1,n∈N*)?{an}是等比數(shù)列.
特別提醒:①前兩種方法是判定等差����、等比數(shù)列的常用方法,而后兩種方法常用于選擇�����、填空題中的判定.②若要判定一個(gè)數(shù)列不是等差(比)數(shù)列�,則只需判定其任意的連續(xù)三項(xiàng)不成等差(比)即可.
[跟蹤訓(xùn)練]
3.(2018·全國(guó)卷Ⅰ)已知數(shù)列{an}滿足a1=1��,nan+1=2(n+1)an.設(shè)bn=.
(1)求b1�,b2���,b3�;
(2)判斷數(shù)列{bn}是否為等比數(shù)列����,并說(shuō)明理由�;
(3)求{an}的通項(xiàng)公式.
[解] (1)由條件可得an+1=an.
將n=1代入得�,a2=4a1,而a1=1�����,
10���、所以,a2=4.
將n=2代入得�,a3=3a2,所以��,a3=12.
從而b1=1��,b2=2��,b3=4.
(2){bn}是首項(xiàng)為1,公比為2的等比數(shù)列.
由條件可得=��,即bn+1=2bn�����,又b1=1��,所以{bn}是首項(xiàng)為1���,公比為2的等比數(shù)列.
(3)由(2)可得=2n-1,所以an=n·2n-1.
數(shù)列求和
[探究問(wèn)題]
1.若數(shù)列{cn}是公差為d的等差數(shù)列�����,數(shù)列{bn}是公比為q(q≠1)的等比數(shù)列�����,且an=cn+bn,如何求數(shù)列{an}的前n項(xiàng)和��?
提示:數(shù)列{an}的前n項(xiàng)和等于數(shù)列{cn}和{bn}的前n項(xiàng)和的和.
2.有些數(shù)列單獨(dú)看求和困難�,但相鄰項(xiàng)結(jié)合
11���、后會(huì)變成熟悉的等差數(shù)列、等比數(shù)列求和.試用此種方法求和:
12-22+32-42+…+992-1002.
提示:12-22+32-42+…+992-1002=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2+3+4+…+99+100)=-5 050.
3.我們知道=-���,試用此公式求和:++…+.
提示:由=-得 ++…+
=1-+-+…+-=1-=.
已知數(shù)列{an}的前n項(xiàng)和Sn=kcn-k(其中c、k為常數(shù))�,且a2=4�,a6=8a3�,
(1)求an�����;
(2)求數(shù)
12、列{nan}的前n項(xiàng)和Tn.
【導(dǎo)學(xué)號(hào):91432242】
思路探究:(1)已知Sn��,據(jù)an與Sn的關(guān)系an=確定an�;(2)若{an}為等比數(shù)列���,則{nan}是由等差數(shù)列和等比數(shù)列的對(duì)應(yīng)項(xiàng)的積構(gòu)成的新數(shù)列,則可用錯(cuò)位相減法求和.
[解] (1)當(dāng)n>1時(shí)���,an=Sn-Sn-1=k(cn-cn-1),
則a6=k(c6-c5)����,
a3=k(c3-c2),
==c3=8���,
∴c=2.
∵a2=4�,即k(c2-c1)=4���,
解得k=2,
∴an=2n.
當(dāng)n=1時(shí)�,a1=S1=2.
綜上所述,an=2n(n∈N*).
(2)nan=n·2n����,
則Tn=2+2·22+3·
13��、23+…+n·2n��,
2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1�,
兩式作差得-Tn=2+22+23+…+2n-n·2n+1�,
Tn=2+(n-1)·2n+1.
母題探究:1.(變結(jié)論)例題中的條件不變���,(2)中“求數(shù)列{nan}的前n項(xiàng)和Tn”變?yōu)椤扒髷?shù)列{n+an}的前n項(xiàng)和Tn”.
[解] 由題知Tn=1+2+2+22+3+23+…+n+2n
=(1+2+3+…+n)+(2+22+…+2n)
=+
=2n+1-2+.
2.(變結(jié)論)例題中的條件不變,將(2)中“求數(shù)列{nan}的前n項(xiàng)和Tn”變?yōu)椤扒髷?shù)列的前n項(xiàng)和Tn”.
[解] 由題T
14、n=+++…+���,①
Tn=++…++,②
①-②得:
Tn=+++…+-
=-=1-n-�,
∴Tn=2--=2-.
[規(guī)律方法] 數(shù)列求和問(wèn)題一般轉(zhuǎn)化為等差數(shù)列或等比數(shù)列的前n項(xiàng)和問(wèn)題或已知公式的數(shù)列求和�,不能轉(zhuǎn)化的再根據(jù)數(shù)列通項(xiàng)公式的特點(diǎn)選擇恰當(dāng)?shù)姆椒ㄇ蠼?,一般常見(jiàn)的求和方法有:
(1)公式法:利用等差數(shù)列或等比數(shù)列前n項(xiàng)和公式;
(2)分組求和法:把一個(gè)數(shù)列分成幾個(gè)可以直接求和的數(shù)列.
(3)裂項(xiàng)(相消)法:有時(shí)把一個(gè)數(shù)列的通項(xiàng)公式分成兩項(xiàng)差的形式���,
相加過(guò)程消去中間項(xiàng)��,只剩有限項(xiàng)再求和.
(4)錯(cuò)位相減法:適用于一個(gè)等差數(shù)列和一個(gè)等比數(shù)列對(duì)應(yīng)項(xiàng)相乘構(gòu)成
的數(shù)列求和.
(5)倒序相加法:例如���,等差數(shù)列前n項(xiàng)和公式的推導(dǎo).
- 8 -
 2018年秋高中數(shù)學(xué) 第二章 數(shù)列 階段復(fù)習(xí)課 第2課 數(shù)列學(xué)案 新人教A版必修5
2018年秋高中數(shù)學(xué) 第二章 數(shù)列 階段復(fù)習(xí)課 第2課 數(shù)列學(xué)案 新人教A版必修5