2022高中物理 牛頓定律應(yīng)用專題 9 巧用整體法和隔離法解決共點(diǎn)力問題學(xué)案 新人教版必修1

《2022高中物理 牛頓定律應(yīng)用專題 9 巧用整體法和隔離法解決共點(diǎn)力問題學(xué)案 新人教版必修1》由會員分享，可在線閱讀，更多相關(guān)《2022高中物理 牛頓定律應(yīng)用專題 9 巧用整體法和隔離法解決共點(diǎn)力問題學(xué)案 新人教版必修1（4頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

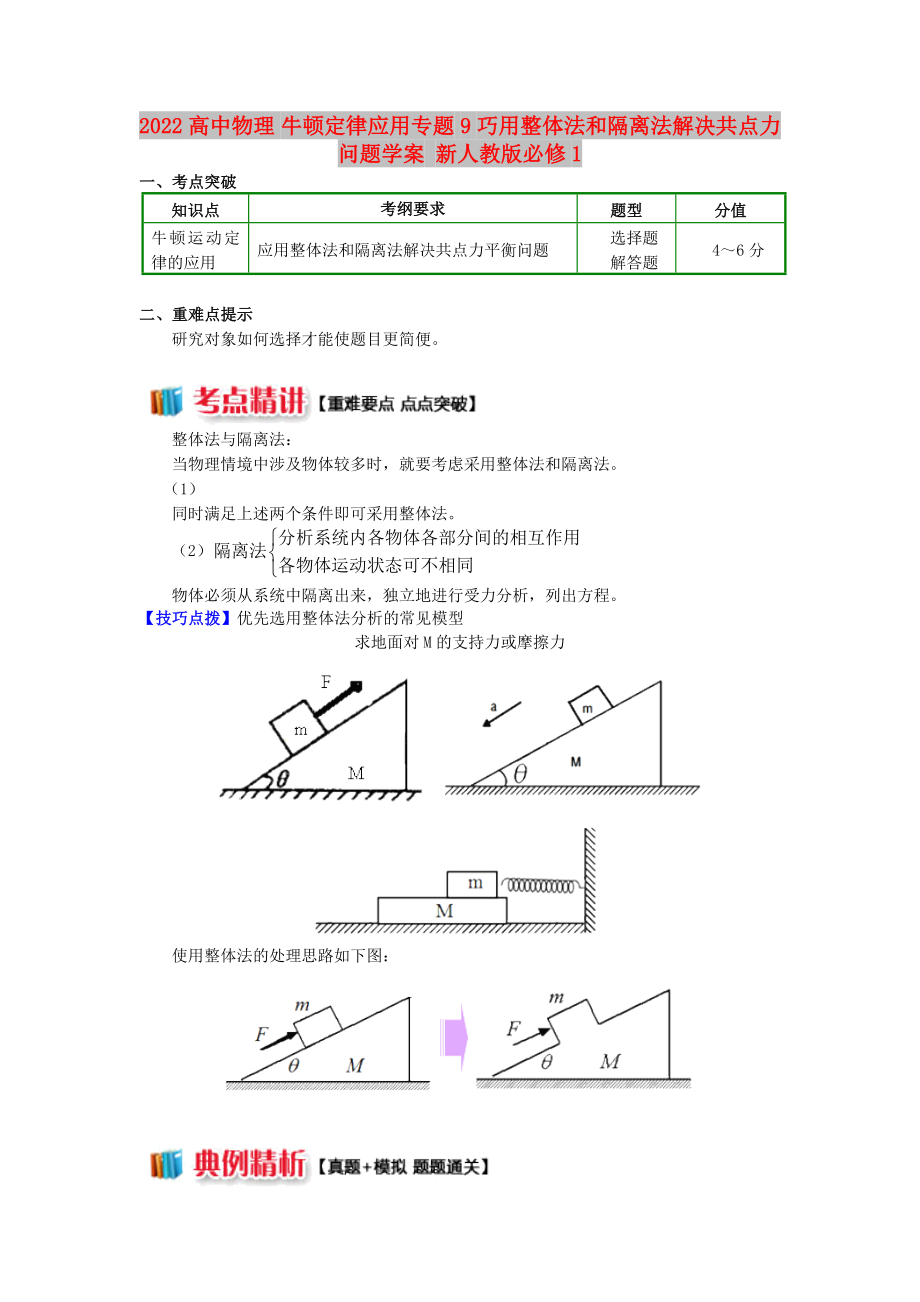
1、2022高中物理 牛頓定律應(yīng)用專題 9 巧用整體法和隔離法解決共點(diǎn)力問題學(xué)案 新人教版必修1 一、考點(diǎn)突破 知識點(diǎn) 考綱要求 題型 分值 牛頓運(yùn)動定律的應(yīng)用 應(yīng)用整體法和隔離法解決共點(diǎn)力平衡問題 選擇題 解答題 4～6分 二、重難點(diǎn)提示 研究對象如何選擇才能使題目更簡便。 整體法與隔離法： 當(dāng)物理情境中涉及物體較多時(shí)，就要考慮采用整體法和隔離法。 （1） 同時(shí)滿足上述兩個(gè)條件即可采用整體法。 （2） 物體必須從系統(tǒng)中隔離出來，獨(dú)立地進(jìn)行受力分析，列出方程。 【技巧點(diǎn)撥】優(yōu)先選用整體法分析的常見模型 求地面對M的支持力或摩擦力 使用

2、整體法的處理思路如下圖： 例題1 如圖所示，用完全相同的輕彈簧A、B、C將兩個(gè)相同的小球連接并懸掛，小球處于靜止?fàn)顟B(tài)，彈簧A與豎直方向的夾角為30°，彈簧C水平，則彈簧A、C的伸長量之比為（　?。? A.∶4　　　　　　　 B。4∶ C. 1∶2 D. 2∶1 思路分析：這是典型的平衡模型，解題的要點(diǎn)是對兩小球進(jìn)行受力分析、列平衡方程，若取兩小球作為一個(gè)整體來研究會更方便。 解法1：分別對兩小球受力分析，如圖所示 FAsin 30°－FBcos θ＝0 F′Bcos θ－FC＝0 FB＝F′B 得FA＝2FC，即彈簧A、C的伸長量之比為2∶1，選項(xiàng)D正

3、確； 解法2：將兩球作為一個(gè)整體，進(jìn)行受力分析，如圖所示 由平衡條件知 即FA＝2FC 故選項(xiàng)D正確。 答案：D 例題2 如圖所示，質(zhì)量為M、半徑為R的半球形物體A放在水平地面上，通過最高點(diǎn)處的釘子用水平細(xì)線拉住一質(zhì)量為m、半徑為r的光滑球B，以下說法正確的是（　?。? A. A對地面的壓力等于（M＋m）g B. A對地面的摩擦力方向向左 C. B對A的壓力大小為 D. 細(xì)線對小球的拉力大小為 思路分析：（1）分析物體A與地面間的作用力可用整體法。 （2）分析球的受力情況要用隔離法。 解：對整體受力分析，可以確定A與地面間不存在摩擦力，地面對A的支持力等于

4、A、B的總重力；再對B受力分析，借助兩球心及釘子位置組成的三角形，根據(jù)幾何關(guān)系和力的合成分解知識求得A、B間的彈力大小為，細(xì)線的拉力大小為。 答案：AC 例題3 如圖所示，截面為三角形的木塊a上放置一鐵塊b，三角形木塊豎直邊靠在豎直且粗糙的墻面上，現(xiàn)用豎直向上的作用力F，推動木塊與鐵塊一起向上勻速運(yùn)動，運(yùn)動過程中鐵塊與木塊始終保持相對靜止，則下列說法正確的是 （　?。? A. 木塊a與鐵塊b間一定存在摩擦力 B. 木塊與豎直墻面間一定存在水平彈力 C. 木塊與豎直墻面間一定存在摩擦力 D. 豎直向上的作用力F大小一定大于鐵塊與木塊的重力之和 思路分析：鐵塊b處于平衡

5、狀態(tài)，故鐵塊b受重力、斜面對它的垂直斜面向上的支持力和沿斜面向上的靜摩擦力，選項(xiàng)A正確；將a、b看作一個(gè)整體，豎直方向：F＝Ga＋Gb，選項(xiàng)D錯(cuò)誤；整體水平方向不受力，故木塊與豎直墻面間不存在水平彈力，沒有彈力也就沒有摩擦力，選項(xiàng)B、C均錯(cuò)。 答案：A 【綜合拓展】拉密定理的應(yīng)用 三力平衡時(shí)，三個(gè)力的合力為零，即構(gòu)成了一個(gè)閉合的三角形，若由題設(shè)條件尋找到角度之間的關(guān)系，即可用拉密定理列式快速求解。 針對訓(xùn)練：一盞電燈重力為G，懸于天花板上A點(diǎn)，在電線O處系一細(xì)線OB，使電線OA與豎直方向的夾角為β＝30°，如圖所示?，F(xiàn)保持β角不變，緩慢調(diào)整OB方向至OB線上拉力最小為止，此時(shí)OB與水平方向的夾角α等于多少？最小拉力是多少？ 思路分析：對電燈受力分析如圖所示 據(jù)三力平衡特點(diǎn)可知：OA、OB對O點(diǎn)的作用力TB、TA的合力T與G等大反向， 即T＝G　 ① 在△OTBT中，∠TOTB＝90°－α 又∠OTTB＝∠TOA＝β， 故∠OTBT＝180°－(90°－α)－β＝90°＋α－β 由正弦定理得 ② 聯(lián)立①②解得 因β不變，故當(dāng)α＝β＝30°時(shí)，TB最小，且TB＝Gsinβ＝