中考數(shù)學(xué)第二輪專題復(fù)習(xí) 規(guī)律探索問(wèn)題

《中考數(shù)學(xué)第二輪專題復(fù)習(xí) 規(guī)律探索問(wèn)題》由會(huì)員分享，可在線閱讀，更多相關(guān)《中考數(shù)學(xué)第二輪專題復(fù)習(xí) 規(guī)律探索問(wèn)題（10頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

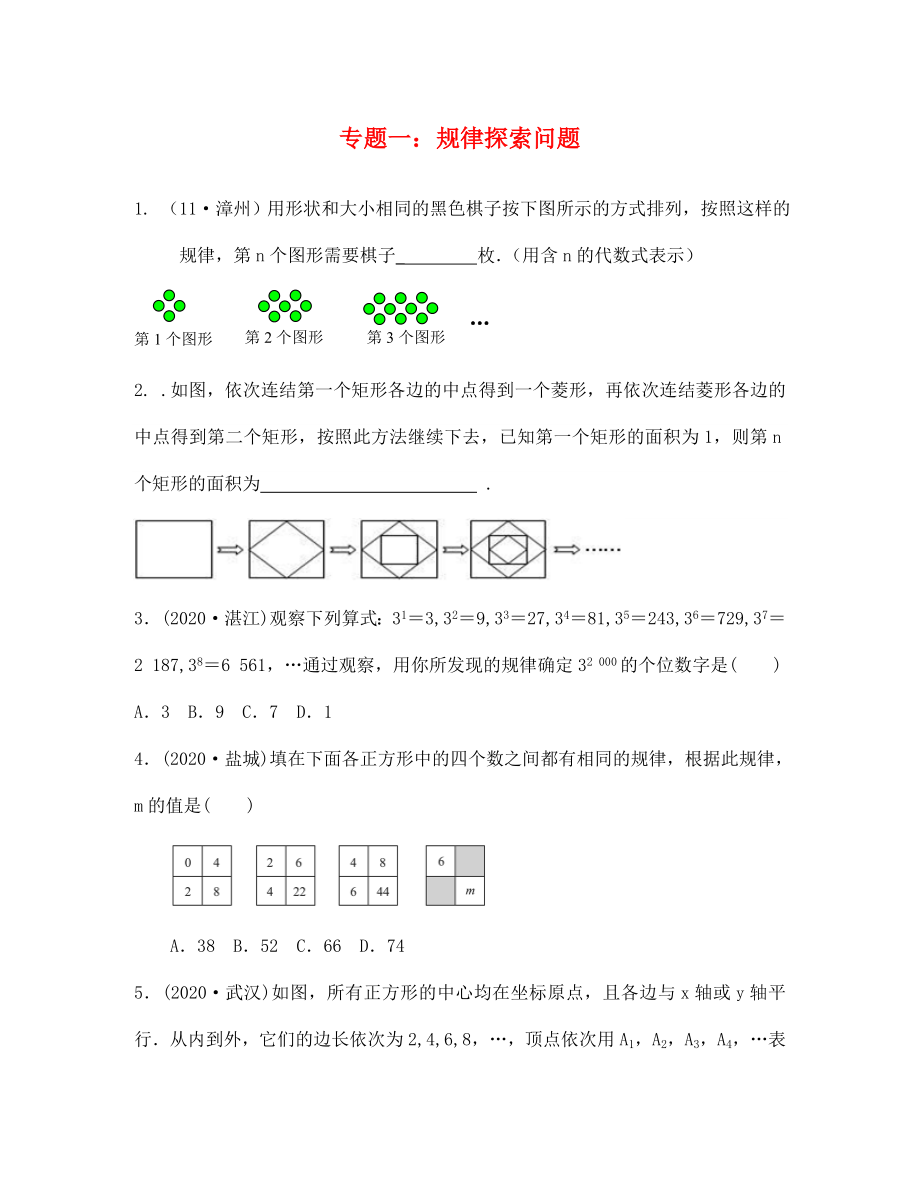
1、專題一：規(guī)律探索問(wèn)題 1. （11·漳州）用形狀和大小相同的黑色棋子按下圖所示的方式排列，按照這樣的規(guī)律，第n個(gè)圖形需要棋子_ 枚．（用含n的代數(shù)式表示） 第1個(gè)圖形 第2個(gè)圖形 第3個(gè)圖形 … 2. .如圖，依次連結(jié)第一個(gè)矩形各邊的中點(diǎn)得到一個(gè)菱形，再依次連結(jié)菱形各邊的中點(diǎn)得到第二個(gè)矩形，按照此方法繼續(xù)下去，已知第一個(gè)矩形的面積為1，則第n個(gè)矩形的面積為 . 3．(2020·湛江)觀察下列算式：31＝3,32＝9,33＝27,34＝81,35＝243,36＝729,37＝2 187,38＝6 561，…通過(guò)

2、觀察，用你所發(fā)現(xiàn)的規(guī)律確定32 000的個(gè)位數(shù)字是(　　) A．3 B．9 C．7 D．1 4．(2020·鹽城)填在下面各正方形中的四個(gè)數(shù)之間都有相同的規(guī)律，根據(jù)此規(guī)律，m的值是(　　) A．38 B．52 C．66 D．74 5．(2020·武漢)如圖，所有正方形的中心均在坐標(biāo)原點(diǎn)，且各邊與x軸或y軸平行．從內(nèi)到外，它們的邊長(zhǎng)依次為2,4,6,8，…，頂點(diǎn)依次用A1，A2，A3，A4，…表示，則頂點(diǎn)A55的坐標(biāo)是(　　) A．(13,13) B．(－13，－13) C．(14,14) D．(－14，－14) 6．(2020·廣東)閱讀下列材料： 1×

3、2＝(1×2×3－0×1×2)， 2×3＝(2×3×4－1×2×3)， 3×4＝(3×4×5－2×3×4)， 由以上三個(gè)等式相加，可得 1×2＋2×3＋3×4＝×3×4×5＝20. 讀完以上材料，請(qǐng)你計(jì)算下列各題： (1)1×2＋2×3＋3×4＋…＋10×11(寫(xiě)出過(guò)程)； (2)1×2＋2×3＋3×4＋…＋n×(n＋1)＝________； (3)1×2×3＋2×3×4＋3×4×5＋…＋7×8×9＝________. 7．(2020·眉山)如圖，將第一個(gè)圖(圖①)所示的正三角形連結(jié)各邊中點(diǎn)進(jìn)行分割，得到第二個(gè)圖(圖②)；再將第二個(gè)圖中最中間的小正三角形按同樣的方式進(jìn)行分割，

4、得到第三個(gè)圖(圖③)；再將第三個(gè)圖中最中間的小正三角形按同樣的方式進(jìn)行分割，…則得到的第五個(gè)圖中，共有________個(gè)正三角形． 8．(2020·龍巖)如圖是圓心角為30°，半徑分別是1、3、5、7、…的扇形組成的圖形，陰影部分的面積依次記為S1、S2、S3、…，則S50＝________.(結(jié)果保留π) 解答題 例1．(15分)(2020·杭州)給出下列命題： 命題1：點(diǎn)(1,1)是直線y＝x與雙曲線y＝的一個(gè)交點(diǎn)； 命題2：點(diǎn)(2,4)是直線y＝2x與雙曲線y＝的一個(gè)交點(diǎn)； 命題3：點(diǎn)(3,9)是直線y＝3x與雙曲線y＝的一個(gè)交點(diǎn)；…… (1)請(qǐng)觀察上面

5、的命題，猜想出命題n(n是正整數(shù))； (2)證明你猜想的命題n是正確的． 例2．某數(shù)學(xué)興趣小組開(kāi)展了一次活動(dòng)，過(guò)程如下： 設(shè)∠BAC=θ（0°＜θ＜90°）現(xiàn)把小棒依次擺放在兩射線AB，AC之間，并使小棒兩端分別落在兩射線上． 活動(dòng)一： 如圖甲所示，從點(diǎn)A1開(kāi)始，依次向右擺放小棒，使小棒與小棒在端點(diǎn)處互相垂直，A1A2為第1根小棒． 數(shù)學(xué)思考： （1）小棒能無(wú)限擺下去嗎？答：___________ ．（填“能“或“不能”） （2）設(shè)AA1=A1A2=A2A3=1． ①θ=_______ 度； ②若記小棒A2n-1A2n的長(zhǎng)度為an（n為正整數(shù)，如A1A2

6、=a1，A3A4=a2，…），求出此時(shí)a2，a3的值，并直接寫(xiě)出an（用含n的式子表示）． 活動(dòng)二： 如圖乙所示，從點(diǎn)A1開(kāi)始，用等長(zhǎng)的小棒依次向右擺放，其中A1A2為第1根小棒，且A1A2=AA1． 數(shù)學(xué)思考： （3）若已經(jīng)向右擺放了3根小棒，則θ1=______ ，θ2=______ ，θ3=_________ （用含θ的式子表示）； （4）若只能擺放4根小棒，求θ的范圍． 專題一：規(guī)律探索作業(yè)： 姓名________________ 1．(2020·福州)如圖，

7、直線y＝x，點(diǎn)A1坐標(biāo)為(1,0)，過(guò)點(diǎn)A1作x軸的垂線交直線于點(diǎn)B1，以原點(diǎn)O為圓心，OB1長(zhǎng)為半徑畫(huà)弧交x軸于點(diǎn)A2；再過(guò)點(diǎn)A2作x軸的垂線交直線于點(diǎn)B2，以原點(diǎn)O為圓心，OB2長(zhǎng)為半徑畫(huà)弧交x軸于點(diǎn)A3，…，按此作法進(jìn)行下去，點(diǎn)A5的坐標(biāo)為_(kāi)_______． 2．(2020·十堰)如圖，n＋1個(gè)上底、兩腰皆為1，下底長(zhǎng)為2的等腰梯形的下底均在同一直線上，設(shè)四邊形P1M1N1N2的面積為S1，四邊形P2M2N2N3的面積為S2，…，四邊形 PnMnNnNn＋1的面積為Sn，通過(guò)逐一計(jì)算S1，S2，…，可得Sn＝________. 3．(2020·連云港)如

8、圖，△ABC的面積為1，分別取AC、BC兩邊的中點(diǎn)A1、B1，則四邊形A1ABB1的面積為，再分別取A1C、B1C的中點(diǎn)A2、B2，A2C、B2C的中點(diǎn)A3、B3，依次取下去，……利用這一圖形，能直觀地計(jì)算出＋＋＋…＝________. 4．（2020?江津區(qū)）如圖，四邊形ABCD中，AC=a，BD=b，且AC丄BD，順次連接四邊形ABCD 各邊中點(diǎn)，得到四邊形A1B1C1D1，再順次連接四邊形A1B1C1D1各邊中點(diǎn)，得到四邊形A2B2C2D2…，如此進(jìn)行下去，得到四邊形AnBnCnDn．下列結(jié)論正確的有（　?。? ①四邊形A2B2C2D2是矩形； ②四邊形A4B4C4D4是菱形；

9、③四邊形A5B5C5D5的周長(zhǎng)是 ④四邊形AnBnCnDn的面積是． A、①② B、②③ C、②③④ D、①②③④ 5. 我們把分子為1的分?jǐn)?shù)叫做理想分?jǐn)?shù)，如，，，…， 任何一個(gè)理想分?jǐn)?shù)都可以寫(xiě)成兩個(gè)不同理想分?jǐn)?shù)的和，如=+；=+；=+；…根據(jù)對(duì)上述式子的觀察，請(qǐng)你思考：如果理想分?jǐn)?shù)（n是不小于2的正整數(shù)）=+， 那么a+b=　 ．（用含n的式子表示） 6. 如圖，在△ABC中，∠ACB＝90o，∠A＝30o，BC＝1．過(guò)點(diǎn)C作 CC1⊥AB于C1，過(guò)點(diǎn)C1作C1C2⊥AC于C2，過(guò)點(diǎn)C2作C2C3⊥AB于C3，…， 按此作發(fā)進(jìn)行下去，則AC

10、n＝ ． 7．2002年在北京召開(kāi)的世界數(shù)學(xué)大會(huì)會(huì)標(biāo)圖案是由四個(gè)全等的直角三角形圍成的一個(gè)大正方形，中間的陰影部分是一個(gè)小正方形的“趙爽弦圖”．若這四個(gè)全等的直角三角形有一個(gè)角為30°，頂點(diǎn)、、、…、和、、、…、分別在直線-和軸上，則第個(gè)陰影正方形的面積為 ． 8．(2020·江西)課題：兩個(gè)重疊的正多邊形，其中的一個(gè)繞某一頂點(diǎn)旋轉(zhuǎn)所形成的有關(guān)問(wèn)題． 【實(shí)驗(yàn)與論證】　設(shè)旋轉(zhuǎn)角∠A1A0B1＝α(α<∠A1A0A2)，θ3、θ4、θ5、θ6所示

11、的角如圖所示． (1)用含α的式子表示角的度數(shù)：θ3＝________，θ4＝________，θ5＝________. (2)圖①～圖④中，連結(jié)A0H時(shí)，在不添加其他輔助線的情況下，是否存在與直線A0H垂直且被它平分的線段？若存在，請(qǐng)選擇其中的一個(gè)圖給出證明；若不存在，請(qǐng)說(shuō)明理由； 【歸納與猜想】　設(shè)正n邊形A0A1A2…An－1與正n邊形A0B1B2…Bn－1重合(其中，A1與B1重合)，現(xiàn)將正n邊形A0B1B2…Bn－1繞頂點(diǎn)A0逆時(shí)針旋轉(zhuǎn)α(0°<α<)． (3)設(shè)θn與上述“θ3，θ4，…”的意義一樣，請(qǐng)直接寫(xiě)出θn的度數(shù)． (4)試猜想在正n邊形的情形下，是否存在與直線A0H垂直且被它平分的線段？若存在，請(qǐng)將這條線段用相應(yīng)的頂點(diǎn)字母表示出來(lái)(不要求證明)；若不存在，請(qǐng)說(shuō)明理由．