陜西省高中數(shù)學(xué) 第一章 計數(shù)原理 如何正確使用兩個基本原理解題拓展資料素材 北師大版選修2-3

《陜西省高中數(shù)學(xué) 第一章 計數(shù)原理 如何正確使用兩個基本原理解題拓展資料素材 北師大版選修2-3》由會員分享，可在線閱讀，更多相關(guān)《陜西省高中數(shù)學(xué) 第一章 計數(shù)原理 如何正確使用兩個基本原理解題拓展資料素材 北師大版選修2-3（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、如何正確使用兩個基本原理解題 分類計數(shù)原理和分步計數(shù)原理是分析解決排列組合等問題、推導(dǎo)排列、組合公式的重要依據(jù)，其應(yīng)用非常廣泛、重要。學(xué)好這兩個原理為后面知識的學(xué)習(xí)奠定基礎(chǔ)。 一、 正確區(qū)分兩個原理 1、分類加法計數(shù)原理和分步乘法計數(shù)原理，回答的都是有關(guān)做一件事的不同方法的種數(shù)問題。區(qū)別在于：分類加法計數(shù)原理針對的是“分類”問題，其中各種方法相互獨立，用其中任何一種方法都可以做完這件事；分步乘法計數(shù)原理針對的是“分步”問題，各個步驟中的方法互相依存，只有各個步驟都完成才算做完這件事。 2、兩個基本原理的區(qū)別在于前者――分類加法計數(shù)原理每次得到的是最后結(jié)果；后者――分步乘法計數(shù)原

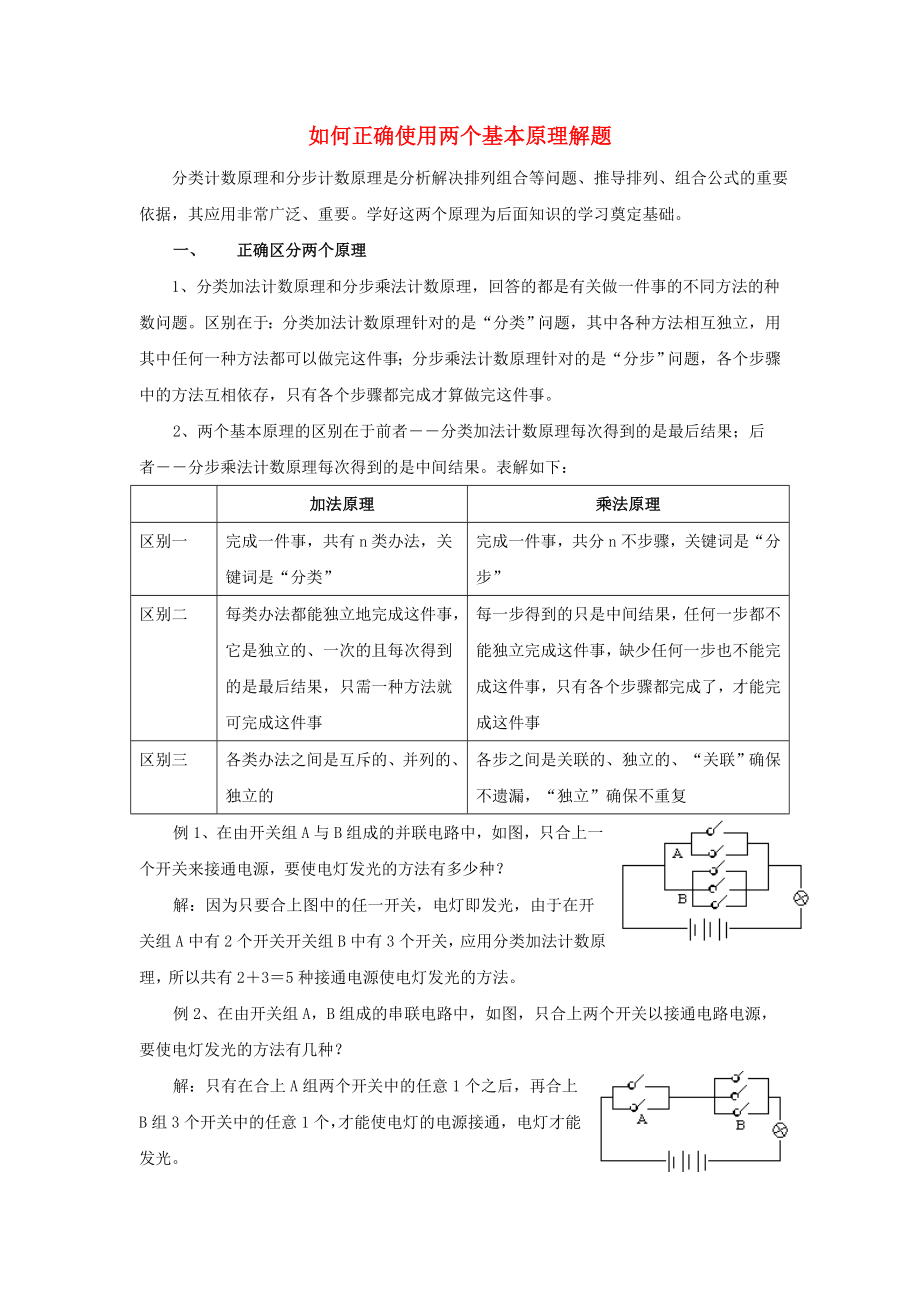
2、理每次得到的是中間結(jié)果。表解如下： 加法原理 乘法原理 區(qū)別一 完成一件事，共有n類辦法，關(guān)鍵詞是“分類” 完成一件事，共分n不步驟，關(guān)鍵詞是“分步” 區(qū)別二 每類辦法都能獨立地完成這件事，它是獨立的、一次的且每次得到的是最后結(jié)果，只需一種方法就可完成這件事 每一步得到的只是中間結(jié)果，任何一步都不能獨立完成這件事，缺少任何一步也不能完成這件事，只有各個步驟都完成了，才能完成這件事 區(qū)別三 各類辦法之間是互斥的、并列的、獨立的 各步之間是關(guān)聯(lián)的、獨立的、“關(guān)聯(lián)”確保不遺漏，“獨立”確保不重復(fù) 例1、在由開關(guān)組A與B組成的并聯(lián)電路中，如圖，只合上一個開關(guān)來接通電源，要使

3、電燈發(fā)光的方法有多少種？ 解：因為只要合上圖中的任一開關(guān)，電燈即發(fā)光，由于在開關(guān)組A中有2個開關(guān)開關(guān)組B中有3個開關(guān)，應(yīng)用分類加法計數(shù)原理，所以共有2＋3＝5種接通電源使電燈發(fā)光的方法。 例2、在由開關(guān)組A，B組成的串聯(lián)電路中，如圖，只合上兩個開關(guān)以接通電路電源，要使電燈發(fā)光的方法有幾種？ 解：只有在合上A組兩個開關(guān)中的任意1個之后，再合上B組3個開關(guān)中的任意1個，才能使電燈的電源接通，電燈才能發(fā)光。 根據(jù)分步乘法計數(shù)原理共有2×3＝6種不同的方法接通電源，使電燈發(fā)光。 點評：通過上面兩道物理并聯(lián)與串聯(lián)的求解，對兩個原理的理解從根本上理解。 二、 應(yīng)用兩原理的關(guān)鍵 1、對于分類加

4、法計數(shù)原理的應(yīng)用問題，需要來分類的問題時，一是要準(zhǔn)確、 透徹地理解題意；二是分類時，必須確定一個分類標(biāo)準(zhǔn)，而分類標(biāo)準(zhǔn)的選擇，則需要在仔細(xì)分析題意的基礎(chǔ)上來確定。 2、對于分步乘法計數(shù)原理的應(yīng)用問題，需要我們自己確定一個分步的步驟，然后依照步驟進(jìn)行操作即可。 例3、三邊長均為整數(shù)，且最大邊長為11的三角形有多少個？ 解：利用三角形兩邊之和大于第三邊的特性，逐類討論。 令兩邊長用x、y表示，且不妨設(shè)，要構(gòu)成三角形，必須 當(dāng)y取11時，x＝1，2，3，……，11，可有11個三角形； 當(dāng)y取10時，x＝2，3，……，10，可有9個三角形； …… 當(dāng)y取6時，x＝6，可有1個三角形，

5、 所以所求三角形的個數(shù)為11＋9＋7＋5＋3＋1＝36個。 例4、求4320的不同的正約數(shù)的個數(shù)。 分析：因為，所以它的正約數(shù)（如15）的質(zhì)因數(shù)必在2、3、5中（如3和5），但該質(zhì)因數(shù)的指數(shù)的取法不同，以此作為分步依據(jù)即可。 解：設(shè)4320的正約數(shù)為，則可取0、1、2、3、4、5；可取0、1、2、3；可取0、1；故所求的正約數(shù)的個數(shù)為6×4×2＝48個。 點評：本題中沒有給出如何尋找4320的正約數(shù)的步驟，需要我們自己來確定，那么如何構(gòu)造這個分步步驟呢？本題解答是從它的一個具體正約數(shù)15入手分析，不難發(fā)現(xiàn)它的質(zhì)因數(shù)為3和5，都在4320的質(zhì)因數(shù)2、3、5中，即15＝3×5，由此推廣到一

6、般有：要確定4320的一個正約數(shù)，只需確定2、3、5的指數(shù)、、即可，從而構(gòu)建一個分步步驟。由此可見，要構(gòu)建一個分步步驟，有時從特例入手分析，有利于我們尋找這個分步步驟。 三、 善用幾種常見方法解決兩原理綜合性問題 對于有些計數(shù)問題的解決，對它們既需要進(jìn)行“分類”，又需要進(jìn)行“分步”，那么此時就要注意綜合運用兩個原理來解決問題。解決這類問題，首先要明確是先“分類”后“分步”，還是先“分步”，后“分類”；其次，在“分類”和“分步”的過程中，均要確定明確的分類標(biāo)準(zhǔn)和分步程序。此外，還需掌握列舉法、樹枝圖法、排序法、模型法來準(zhǔn)確求解綜合性問題。 例5、三人傳球，由甲開始發(fā)球，并作為第1次傳球，經(jīng)過5次傳球后，球仍回到甲手中，則不同的傳球方式共有多少種？ 解：如圖所示： 第一個空與第二個空不能是甲，分三類討論： （1）若第二個空是甲，則第一個空有2種選擇方法，第三個空有2種選擇方法，第四個空僅有1種選擇方法，所以2×2＝4種方法； （2）若第三個空是甲，同上，有2×2＝4種方法； （3）若第二個、第三個空都不填甲，則僅有如下兩種傳球方法： 甲乙丙乙丙甲；甲丙乙丙乙甲. 所以共有4＋4＋2＝10種方法。 點評：在這里以空“□”來構(gòu)造模型，從而使看不見摸不著的動態(tài)傳球問題變得形象直觀起來。