2021年春七年級數(shù)學(xué)下冊 12.2 證明作業(yè)3 （新版）蘇科版

《2021年春七年級數(shù)學(xué)下冊 12.2 證明作業(yè)3 （新版）蘇科版》由會員分享，可在線閱讀，更多相關(guān)《2021年春七年級數(shù)學(xué)下冊 12.2 證明作業(yè)3 （新版）蘇科版（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

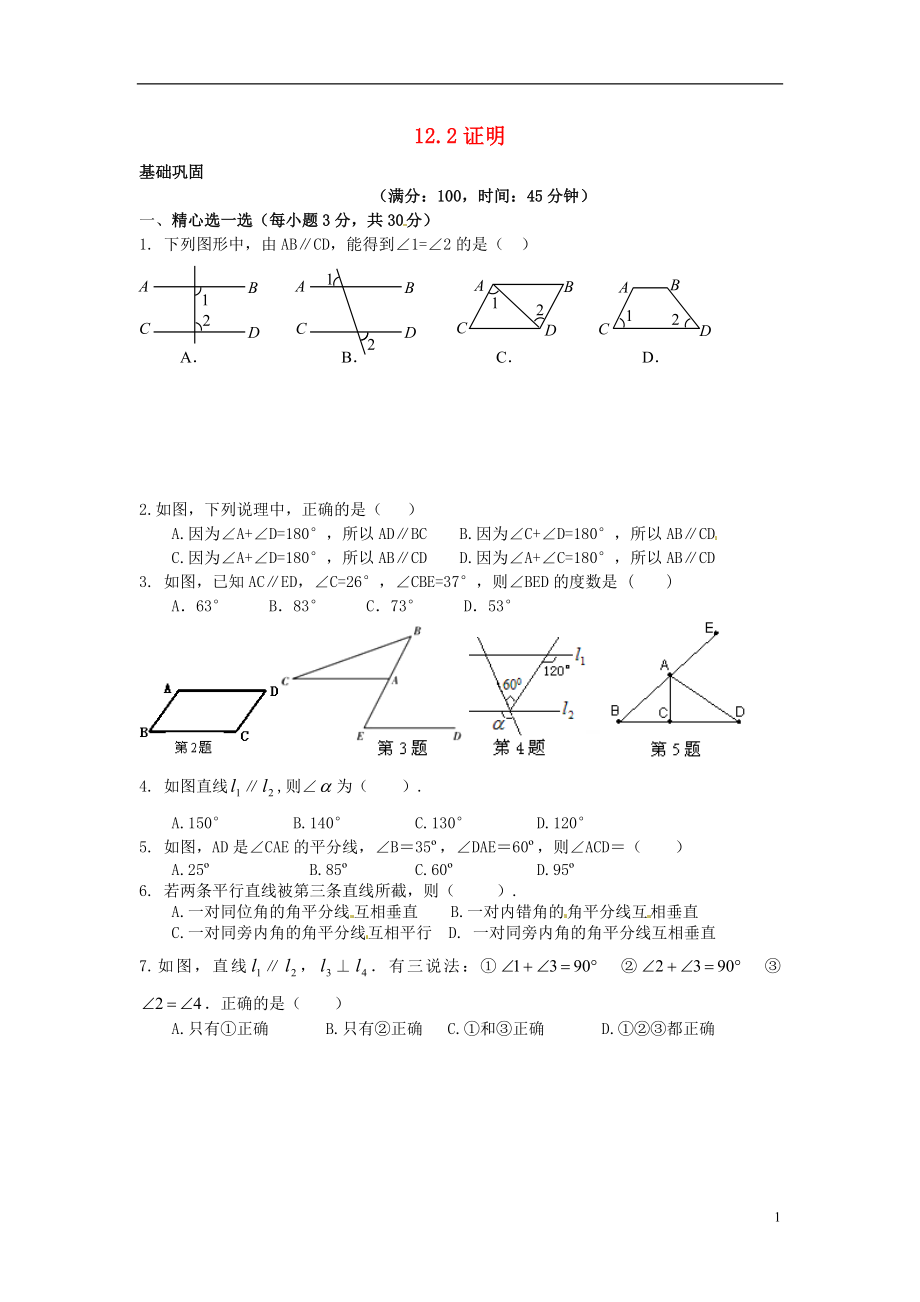
1、 12.2證明 基礎(chǔ)鞏固 （滿分：100，時間：45分鐘） 一、精心選一選（每小題3分，共30分） 1. 下列圖形中，由AB∥CD，能得到∠1=∠2的是（ ） A C B D 1 2 A C B D 1 2 A． B． 1 2 A C B D C． B D C A D． 1 2 2.如圖，下列說理中，正確的是（ ） A.因為∠A+∠D=180°，所以AD∥BC B.因為∠C+∠D=180°，所以AB∥CD C.因為∠A+∠D=180°，所以AB∥CD D.因為∠A+∠C=180°，所以AB∥CD 3

2、. 如圖，已知AC∥ED，∠C=26°，∠CBE=37°，則∠BED的度數(shù)是 ( ) A．63° B．83° C．73° D．53° 4. 如圖直線∥,則∠為（ ）. A.150° B.140° C.130° D.120° 5. 如圖，AD是∠CAE的平分線，∠B＝35o，∠DAE＝60o，則∠ACD＝（　　） 　　A.25o　　　　　　B.85o　　　　C.60o　　　　　D.95o 6. 若兩條平行直線被第三條直線所截，則（ ）. A.一對同位角的角平分線互相垂直 B.一對內(nèi)錯角的角平分線

3、互相垂直 C.一對同旁內(nèi)角的角平分線互相平行 D. 一對同旁內(nèi)角的角平分線互相垂直 7.如圖，直線∥，⊥．有三說法：① ② ③．正確的是（ ） A.只有①正確 B.只有②正確 C.①和③正確 D.①②③都正確 8.如圖，∠1=100°，∠2=145°，那么∠3=（ ） A．55° B．65° C．75° D．85° 9. 如圖，在A、B兩座工廠之間要修建一條筆直的公路，從A地測得B地的走向是南偏東52°，現(xiàn)A.B兩地要同時開工，若干天后公路準(zhǔn)確對接，則B地所修公路的走向應(yīng)該是( ) A.北偏西52° B.南偏東52°

4、 C.西偏北52° D.北偏西38° 10第10題 . 如圖，一條公路修到湖邊時，需拐彎繞道而過，如果第一次拐的角∠A=120°，第二次拐的角∠B是150°，第三次拐的角是∠C，這時的道路恰好和第一次拐彎之前的道路平行，則∠C是（　 ）． A.120° B.130° C.140° D.150° 二、細(xì)心填一填（每小題3分，共30分） 11. 如圖，要得到AB∥CD，只需要添加一個條件，這個條件可以是 ．（填一個你認(rèn)為正確的條件即可） 12. 如圖，AB//CD,CE平分∠ACD，若∠1=250，那么∠2的度數(shù)是

5、 . 13. 如圖所示，AB∥CD，∠ABE＝66°，∠D＝54°，則∠E的度數(shù)為_______________． 14. 如圖AB//CD,直線EF與AB、CD分別相交于E、F兩點，EP平分∠AEF,過點F作FP⊥EP,垂足為P，若∠PEF=30,則∠PFC=__________。 15. 如圖，AB∥，∠1=50°，∠2=110°CD則∠3= ． A B D C 1 2 3 第15題 第17題 第18題 第19題 16. 在△ABC中，若

6、∠A=50°，∠B－∠C＝10°，則∠B＝ ，∠C＝ . 17. 如圖，AD、AE分別是△ABC的角平分線和高，∠B=50°，∠C=70°，則∠BAD= °，∠EAD= °． 18.如圖所示,已知∠1=20°，∠2=25，∠A=35°，則∠BDC的度數(shù)為________. 19.如圖，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=80o，則∠BFD=________. 20．銳角三角形ABC中，3條高相交于點H，若∠BAC＝70°，則∠BHC＝_______. .對于同一平面內(nèi)的三條直線a、b、c，給出下列五個論斷：

7、①a∥b，②b∥c，③a⊥b，④a∥c，⑤a⊥c，以其中兩個論斷為條件，一個論斷為結(jié)論，組成一個你認(rèn)為正確的命題_________． 三、耐心做一做（共40分） 21．(8分) 如圖，BD是△ABC的角平分線，DE∥BC，交AB于點E，∠A=45°，∠BDC=60°，求∠BED的度數(shù). 22.（8分）如圖，在△ABC中，CD⊥AB，垂足為D，點E在BC上，EF⊥AB，垂足為F． （1）CD與EF平行嗎？為什么？ （2）如果∠1=∠2，且∠3=65°，那么∠ACB= °．(寫出計算過程) 23

8、.（8分）閱讀：如圖①，CE∥AB，所以∠1＝∠A，∠2＝∠B.所以∠ACD＝∠1＋∠2＝∠A＋∠B.這是一個有用的事實，請用這個事實在圖②的四邊形ABCD內(nèi)引一條和邊平行的直線，求出∠A＋∠B＋∠C＋∠D的度數(shù)。 24.（8分）某機(jī)器零件的橫截面如圖所示，按要求線段和的延長線相交成直角才算合格，一工人測得∠A=23°，∠D=31°，∠AED=143°，請你幫他判斷該零件是否合格,并說明理由. A B C D E 25.（8分）如圖，ABC的兩邊分別與DEF的兩邊平行，即BA∥ED，BC∥

9、EF． G F E D (乙) C B A (1)在圖(甲)中，射線BA與ED同向，BC與EF也同向； (2)在圖(乙)中，射線BA與ED異向，BC與EF也異向；(3)在圖(丙)中，射線BA與ED同向，BC與EF異向． 問：在上述三種情況下，∠B與∠E的關(guān)系怎樣？為什么？ 能力提高 （滿分：20，時間：15分） 26．(10分) 如圖，已知直線 ∥，且 和、分別交于A、B 兩點，點P在直線AB上． （1）試找出∠1、∠2、∠3之間的關(guān)系并說明理由； （2）當(dāng)點P在A、B兩點之間運(yùn)動時，問∠1、∠2、∠3之間

10、的關(guān)系是否發(fā)生變化？ （3）如果點P在A、B兩點外側(cè)運(yùn)動時，試探究∠1、∠2、∠3 之間的關(guān)系（點P和A、B不重合，只要寫出結(jié)論，不要證明） 27．(10分) 已知如圖∠xOy＝90°，BE是∠ABy的平分線，BE的反向延長線與∠OAB的平分線相交于點C，當(dāng)點A，B分別在射線Ox，Oy上移動時，試問∠ACB的大小是否發(fā)生變化？如果保持不變，請說明理由；如果隨點A，B的移動而變化，請求出變化范圍 《章節(jié)同步測試題（一）》參考答案 基礎(chǔ)訓(xùn)練 一、1～5 BCADD 6～10．DADAD

11、二、11∠1+∠2=180° 12. 50° 13.12° 14. 60° 15. 60° 16. 70°，60° 17. 30°，10° 18.80° 19. 40° 20.答案不唯一：如果a∥b，b∥c，則a∥c；或a⊥b，a⊥c，則b∥c等 三、21. 因為∠BDC=∠A+∠ABD，所以∠ABD =∠BDC-∠A =15°，因為BD平分∠ABC，所以∠ABC=2∠ABD=30°，因為DE∥BC，所以∠BED+∠ABC=180°，所以∠BED=150°. 22. (1) CD∥EF，因為CD⊥AB，EF⊥AB，所以∠BFE=∠BDC=90°，所以CD∥EF. (2)因為C

12、D∥EF，所以∠BCD=∠2，因為∠1=∠2，所以∠1=∠BCD，所以DG∥BC，所以∠3=∠ACB，因為∠3=65°，所以∠ACB=65°. 23.如圖①，因為∠ACB+∠1＋∠2=180°，所以∠A＋∠B+∠ACB=180°，可見三角形三個角的和等于180°. 如圖②，連接AC，根據(jù)上述結(jié)論可知△ABC、△ACD三個角的和都等于180°，所以∠A＋∠B＋∠C＋∠D=360°. 不合格，延長AE交CD于F,延長AB、DC相交于點G，因為∠AED是△DEF的一個外角，所以∠AED=∠DFE+∠D,而∠DFE=∠A+∠G,所以∠AED=∠A+∠G +∠D，所以∠G=∠AED-∠A-∠D=1

13、43°-23°-31°=89°，而按要求線段和的延長線相交成直角才算合格，89°＜90°，所以零件不合格. 25. 圖(甲)中，∠B=∠E，理由是：因為AB∥DE，所以∠B=∠BGD，因為BC∥EF，所以∠E=∠BGD，所以∠B=∠E. 圖(乙) ∠B=∠E，證明略 圖(丙) ∠B+∠E=180°，證明略 能力提高 26. （1）∠1+∠2=∠3，理由是： 過點P作PQ∥，則∠QPC=∠1，因為∥，所以PQ∥，所以∠QPD=∠2，所以∠QPD+∠QPC=∠1+∠2，即∠1+∠2=∠3. （2）不變. （3）∠1+∠2=∠3. 27.不變，∠ACB=∠EBA-∠BAC=∠Aby

14、-∠BAO=∠AOB=45°，隨點A，B的移動，∠ACB的大小不變. 備用題： 1. 如圖，下列推理正確的是（　　） A.∵　∠1＝∠2，∴　AD∥BC B.∵　∠3＝∠4，∴　AB∥CD C.∵　∠3＝∠5，∴　AB∥DC D.∵　∠3＝∠5，∴　AD∥BC 第1題 第2題 第4題 2. 直線a、b都與直線c相交，給出下列條件：①∠1＝∠2；②∠3＝∠6；③∠4＋∠7＝180°；④∠5＋∠8＝180°。其中能判斷a∥b的條件是（ ）。 A.①② B.②④ C.①③④ D.

15、①②③④ 3. 在△ABC中，∠A∶∠B∶∠C = 1∶2∶3，則∠B = 4. 如圖，AD、BE、CF為△ABC的三條角平分線，則：∠1+∠2+∠3=________ 5.如圖，已知∠A=∠1，∠E=∠2，AC⊥CE，求證：AB∥DE. 6. 如圖，已知點A在直線l外，點B,C在直線l上。 （1）點P是△ABC內(nèi)一點，求證：∠P>∠A; （2）試判斷在△ABC外，又和點A在直線l同側(cè)，是否存在一點Q，使∠BQC>∠A,試證明你的結(jié)論。 備用題答案： １.C ２.D ３.60° 4.90° 5.因為∠A=∠1，∠2+∠ACE+∠1=180o，又AC⊥CE，故∠ACE=90o，∴∠1+∠2=90o， ∴∠A+∠2=90o，∴∠ABC=90o，同理∠EDC=90o，∴AB∥DE. 6. （1）延長BP交AC于D，則∠BPC>∠BDC，∠BDC>∠A故∠BPC>∠A (2)在直線l同側(cè)，且在△ABC外，存在點Q，使得∠BQC>∠A成立。此時，只需在AB外，靠近AB中點處取點Q，則∠BQC>∠A。證明略。 7