《【學(xué)霸優(yōu)課】數(shù)學(xué)理一輪對(duì)點(diǎn)訓(xùn)練：612 數(shù)列的通項(xiàng)公式 Word版含解析》由會(huì)員分享，可在線閱讀，更多相關(guān)《【學(xué)霸優(yōu)課】數(shù)學(xué)理一輪對(duì)點(diǎn)訓(xùn)練：612 數(shù)列的通項(xiàng)公式 Word版含解析（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
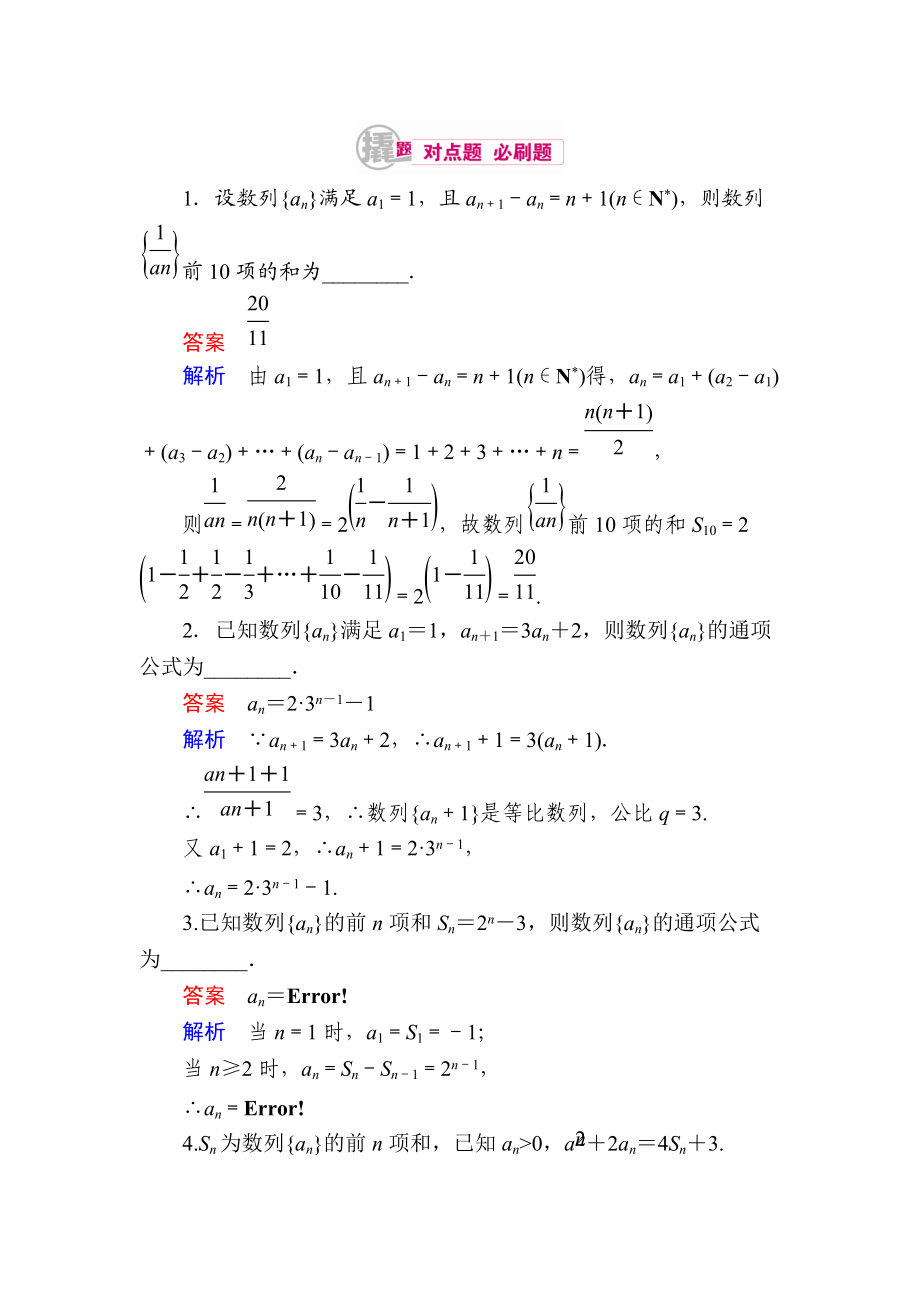
1．設(shè)數(shù)列{an}滿足a1＝1，且an＋1－an＝n＋1(n∈N*)，則數(shù)列前10項(xiàng)的和為_(kāi)_______．
答案
解析 由a1＝1，且an＋1－an＝n＋1(n∈N*)得，an＝a1＋(a2－a1)＋(a3－a2)＋…＋(an－an－1)＝1＋2＋3＋…＋n＝，
則＝＝2，故數(shù)列前10項(xiàng)的和S10＝2＝2＝.
2．已知數(shù)列{an}滿足a1＝1，an＋1＝3an＋2，則數(shù)列{an}的通項(xiàng)公式為_(kāi)_______．
答案 an＝23n－1－1
解析 ∵an＋1＝3an＋2，∴an＋1＋1＝3(an＋1)．
∴＝3，∴數(shù)列{an＋1}是等比數(shù)列，公比q＝3.
又a1＋1＝2，∴
2、an＋1＝23n－1，
∴an＝23n－1－1.
3.已知數(shù)列{an}的前n項(xiàng)和Sn＝2n－3，則數(shù)列{an}的通項(xiàng)公式為_(kāi)_______．
答案 an＝
解析 當(dāng)n＝1時(shí)，a1＝S1＝－1；
當(dāng)n≥2時(shí)，an＝Sn－Sn－1＝2n－1，
∴an＝
4.Sn為數(shù)列{an}的前n項(xiàng)和，已知an>0，a＋2an＝4Sn＋3.
(1)求{an}的通項(xiàng)公式；
(2)設(shè)bn＝，求數(shù)列{bn}的前n項(xiàng)和．
解 (1)由a＋2an＝4Sn＋3，可知a＋2an＋1＝4Sn＋1＋3.
可得a－a＋2(an＋1－an)＝4an＋1，即
2(an＋1＋an)＝a－a＝(an＋1＋an)(a
3、n＋1－an)．
由于an>0，可得an＋1－an＝2.
又a＋2a1＝4a1＋3，解得a1＝－1(舍去)或a1＝3.
所以{an}是首項(xiàng)為3，公差為2的等差數(shù)列，通項(xiàng)公式為an＝2n＋1.
(2)由an＝2n＋1可知
bn＝＝＝.
設(shè)數(shù)列{bn}的前n項(xiàng)和為T(mén)n，則
Tn＝b1＋b2＋…＋bn
＝＝.
5．正項(xiàng)數(shù)列{an}的前n項(xiàng)和Sn滿足：S－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求數(shù)列{an}的通項(xiàng)公式an；
(2)令bn＝，數(shù)列{bn}的前n項(xiàng)和為T(mén)n.證明：對(duì)于任意的n∈N*，都有Tn<.
解 (1)由S－(n2＋n－1)Sn－(n2＋n)＝0，
得[Sn－(n2＋n)](Sn＋1)＝0.
由于{an}是正項(xiàng)數(shù)列，所以Sn>0，Sn＝n2＋n.
于是a1＝S1＝2，當(dāng)n≥2時(shí)，an＝Sn－Sn－1＝n2＋n－(n－1)2－(n－1)＝2n.
綜上，數(shù)列{an}的通項(xiàng)公式為an＝2n.
(2)由于an＝2n，故bn＝＝＝.
Tn＝1－＋－＋－＋…＋－＋－＝1＋－－<＝.
【學(xué)霸優(yōu)課】數(shù)學(xué)理一輪對(duì)點(diǎn)訓(xùn)練：612 數(shù)列的通項(xiàng)公式 Word版含解析
